Multivariate Inputs and Outputs

Often, we want to have our network map multivariate inputs $\mathbf{x}=[x_1,x_2,\dots ,x_{D_i}{]}^T$ to multivariate output predictions $\mathbf{y}=[y_1,y_2,\dots ,y_{D_o}{]}^T$.

Multivariate Outputs

To extend the network to multivariate outputs $\mathbf{y}$, we simply use a different linear function of the hidden units for each output. So, a network with a scalar input $x$, four hidden units $h_1,h_2,h_3,h_4$, and a 2D multivariate output $\mathbf{y}=[y_1,y_2{]}^T$ would be defined as

$$\begin{array}{rl}{h}_1& =a[{\theta }_{10}+{\theta }_{11}x]\\ h_2& =a[{\theta }_{20}+{\theta }_{21}x]\\ h_3& =a[{\theta }_{30}+{\theta }_{31}x]\\ h_4& =a[{\theta }_{40}+{\theta }_{41}x]\end{array}$$

and

$$\begin{array}{rl}{y}_1& ={\varphi }_{10}+{\varphi }_{11}{h}_1+{\varphi }_{12}{h}_2+{\varphi }_{13}{h}_3+{\varphi }_{14}{h}_4\\ y_2& ={\varphi }_{20}+{\varphi }_{11}{h}_1+{\varphi }_{22}{h}_2+{\varphi }_{23}{h}_3+{\varphi }_{24}{h}_4\end{array}$$

The two outputs are two different linear functions of the hidden units.

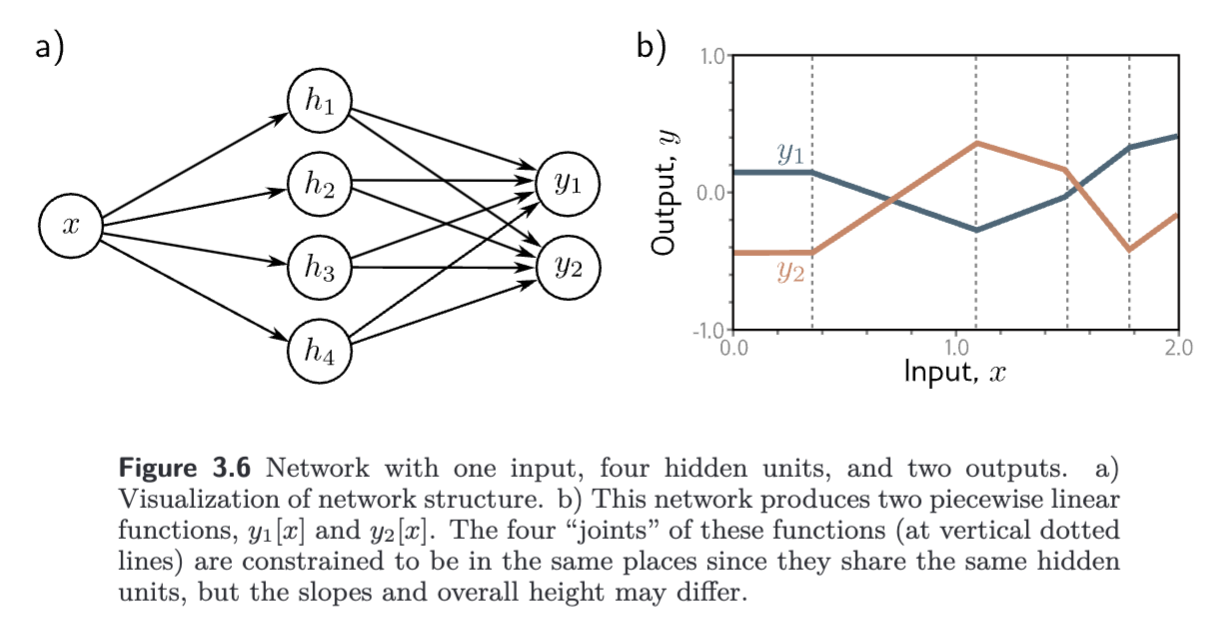
• Recall (from Shallow Neural Network) that the joints in the piecewise functions depend on where the initial functions ${\theta }_{\bullet 0}+{\theta }_{\bullet 1}x$ are clipped by the ReLU functions $a[\bullet ]$ at the hidden units.
• Since both outputs $y_1$ and $y_2$ are different linear functions of the same four hidden units, the four joints are at the same places.
• However, the slopes of the linear regions and the overall vertical offset can differ, since these are applied after the ReLU.

Multivariate Inputs

For multi variate inputs $\mathbf{x}$, we extend the linear relations between the input and the hidden units. So, a network with two inputs $\mathbf{x}=[x_1,x_2{]}^T$ and a scalar output $y$ might have 3 hidden units defined by:

$$\begin{array}{rl}{h}_1& =a[{\theta }_{10}+{\theta }_{11}{x}_1+{\theta }_{12}{x}_2]\\ h_2& =a[{\theta }_{20}+{\theta }_{21}{x}_1+{\theta }_{22}{x}_2]\\ h_3& =a[{\theta }_{30}+{\theta }_{31}{x}_1+{\theta }_{32}{x}_2]\end{array}$$

where there is now one slope parameter for each input. The hidden units are combined to form the output in the usual way:

$$y={\varphi }_0+{\varphi }_1{h}_1+{\varphi }_2{h}_2+{\varphi }_3{h}_3$$

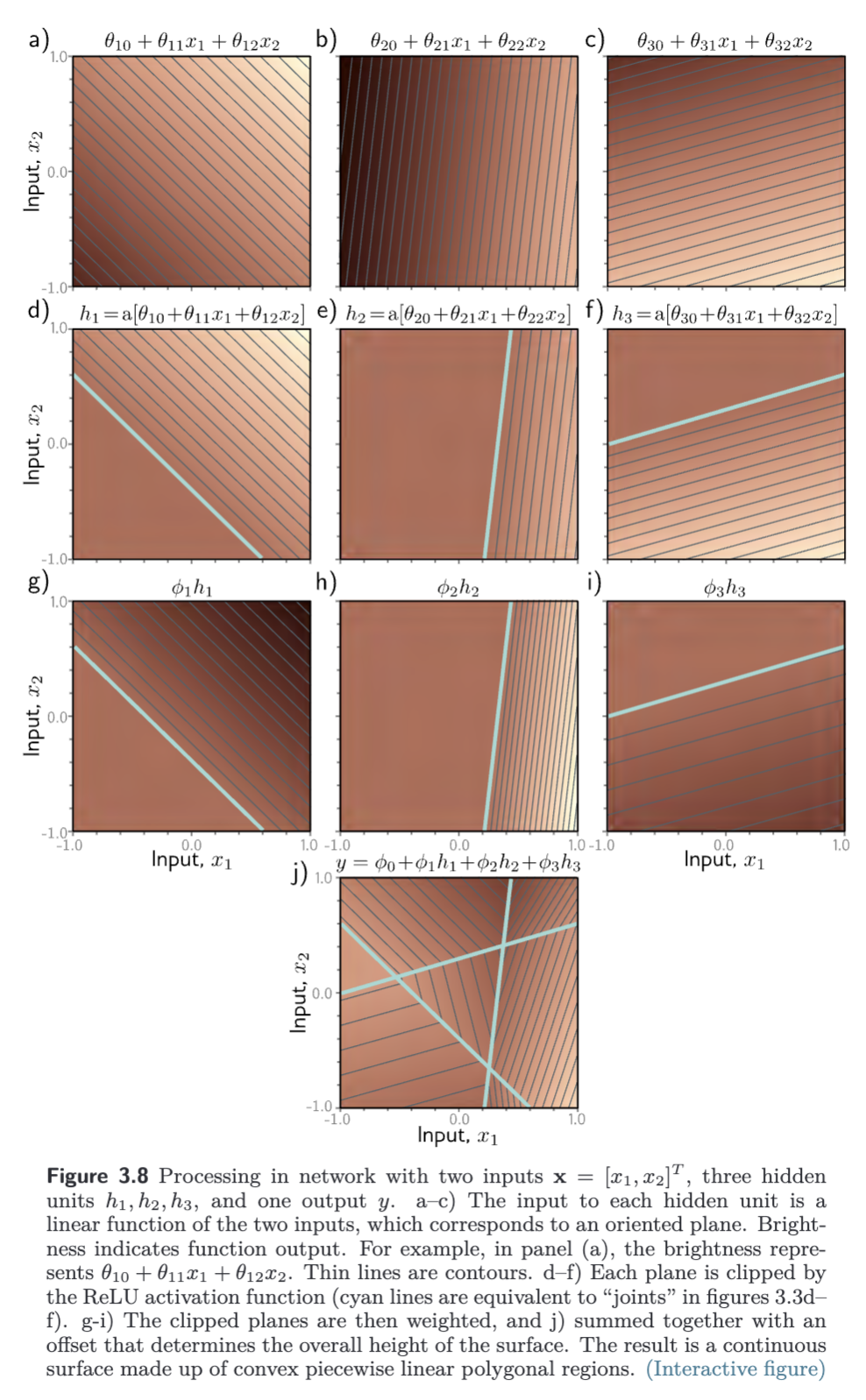
• Each hidden unit receives a linear combination of the two inputs, which forms an oriented plane in the 3D input/output space.
• The activation function clips the negative values of these planes to zero.
• The clipped planes are then recombined in a second linear function to create a continuous piecewise linear surface consisting of convex polygonal regions.
• Each region corresponds to a different activation pattern. For example, in the central triangular region, the 1st and 3rd hidden units are active, with the 2nd inactive.

With more than 2 inputs, the visualization becomes difficult, but the interpretation is similar; the output is just a continuous piecewise linear function of the output, where the linear regions are now convex polytopes in the multi-dimensional input space.