Linear Regions Per Parameter for Neural Network

Shallow Networks

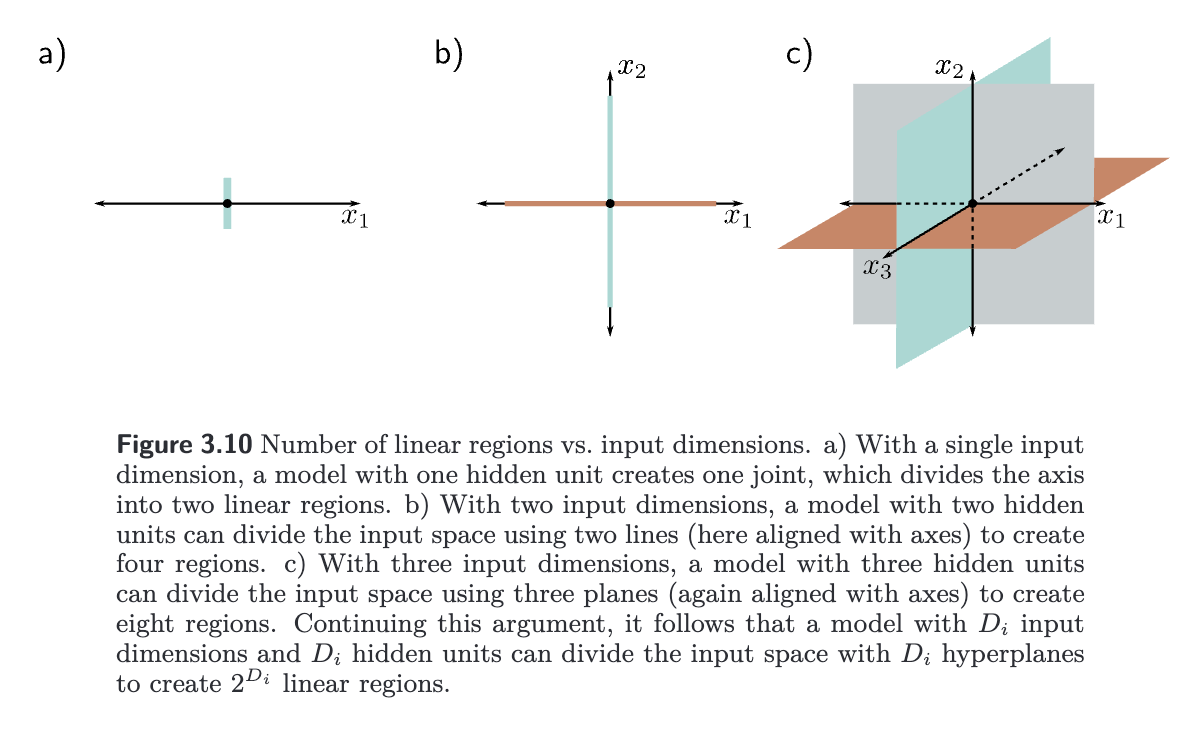
In a shallow network, as the input dimensions grow, the number of linear regions increases rapidly. Each hidden unit defines a hyperplane ($n-1$ dimensional plane) that delineates the part of the space where this unit is active from the part it is not. If we had the same number of hidden units as input dimensions $D_i$, we could align each hyperplane with one of the coordinate axes. For two input dimensions, this would divide the space into four quadrants. For three dimensions, this would create eight octants, and for $D_i$ dimensions, this would create $2^{D_i}$ orthants. hallow neural networks usually have more hidden units than input dimensions, so they typically create more than $2^{D_i}$ linear regions.

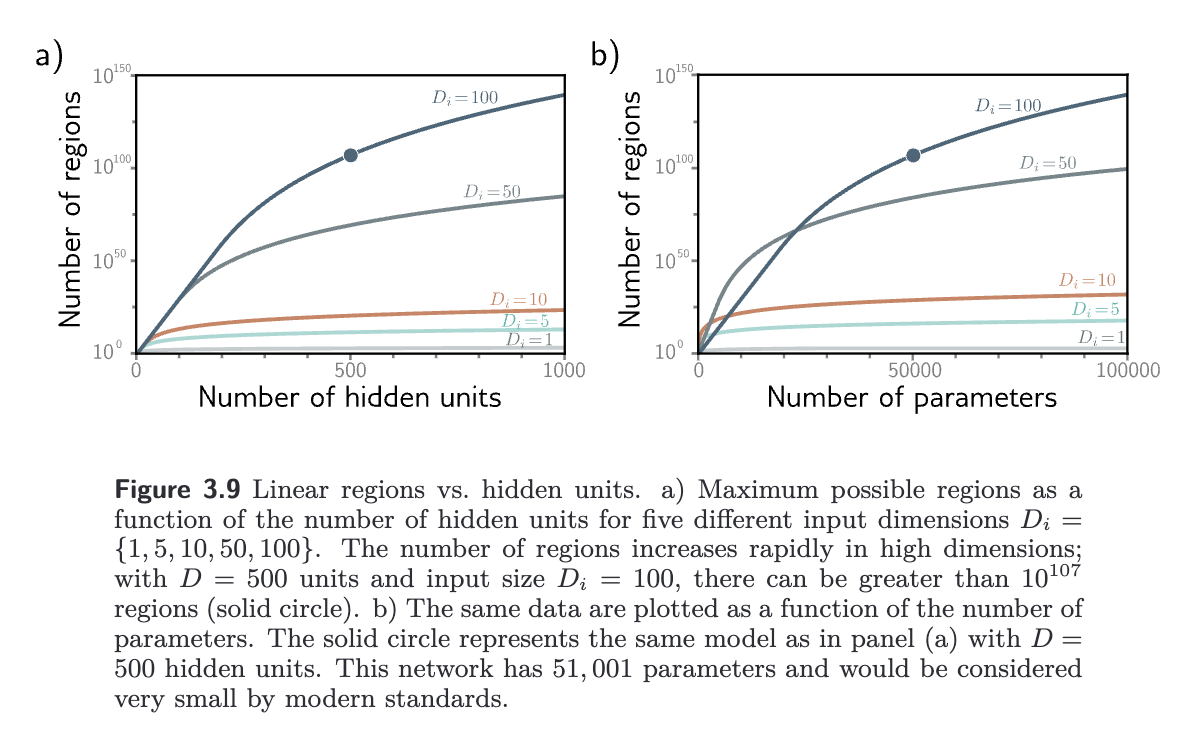
Zavslavsky’s formula: The number of regions created by $D$ hyperplanes in the $D_i\le D$-dimensional input space is at most

$$\sum _{j=0}^{D_i}\left(\genfrac{}{}{0ex}{}{D}{j}\right)$$

which is a sum of binomial coefficients.

As a rule of thumb, shallow neural networks almost always have a larger number $D$ of hidden units than input dimensions $D_i$ and create between $2D_i$ and $2D$ linear regions.

Deep Networks

A shallow network with one input, one output, and $D>2$ hidden units can create up to $D+1$ linear regions and is defined by