Implicit Regularization

Neither gradient descent nor stochastic gradient descent moves neutrally to the minimum of the loss function; each exhibits a preference for some solutions over others. This is known as implicit regularization.

Implicit regularization in gradient descent

Consider a continuous version of gradient descent where the step size is infinitesimal. The change in parameters $\varphi$ would be governed by the differential equation:

$$\frac{d\varphi }{dt}=-\frac{\partial L}{\partial \varphi }$$

Gradient descent approximates this process with a series of discrete steps of size $\alpha$:

$${\varphi }_{t+1}={\varphi }_t-\alpha \frac{\partial L[{\varphi }_t]}{\partial \varphi }$$

This discretization causes a deviation from the continuous path.

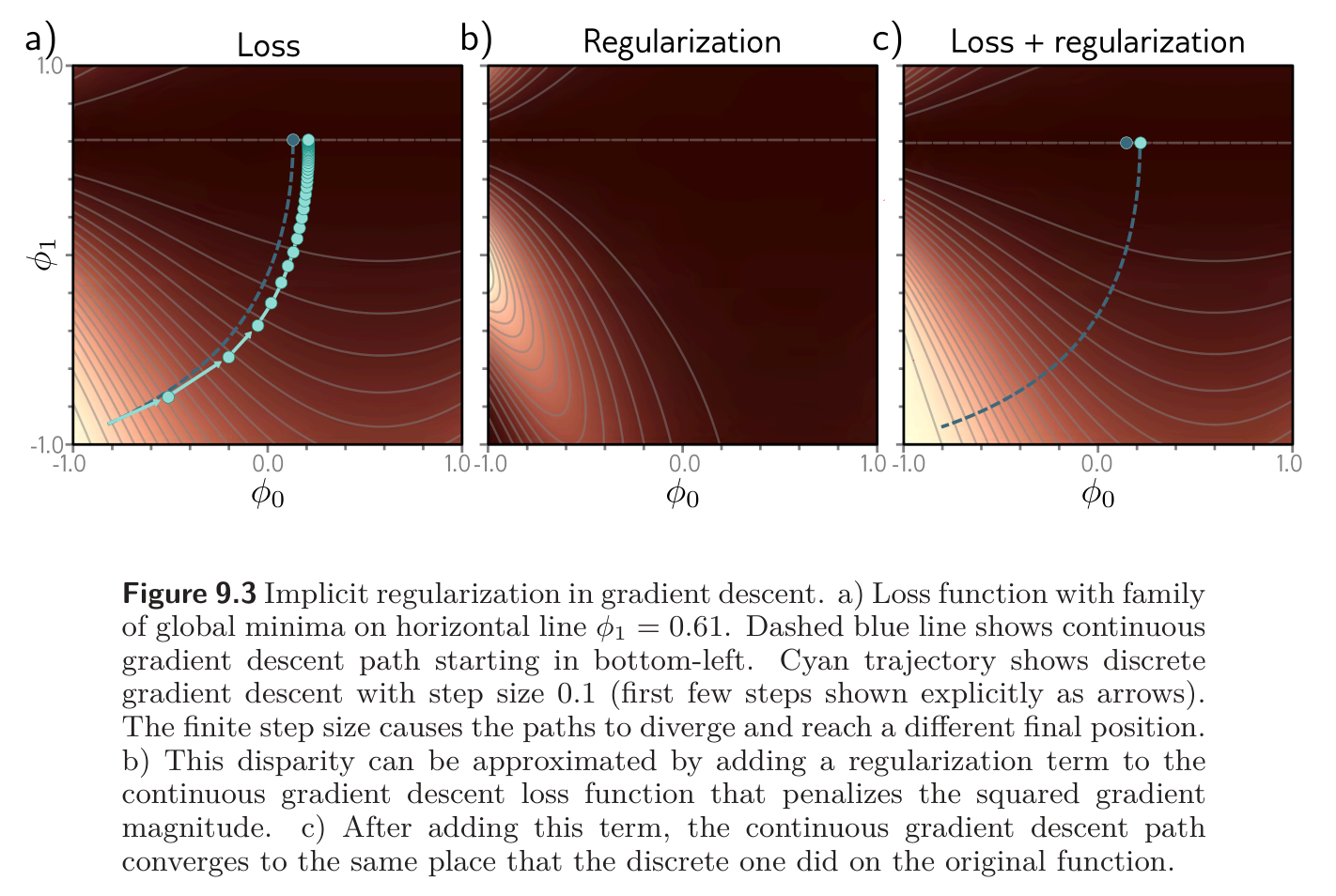
This deviation can be understood by deriving a modified loss term $\tilde{L}$ for the continuous case that arrives at the same places as the discretized version on the original loss $L$. It can be shown that this modified loss is

$${\tilde{L}}_{GD}[\varphi ]=L[\varphi ]+\frac{\alpha }{4}\left|\right|\frac{\partial L}{\partial \varphi }|{|}^2$$

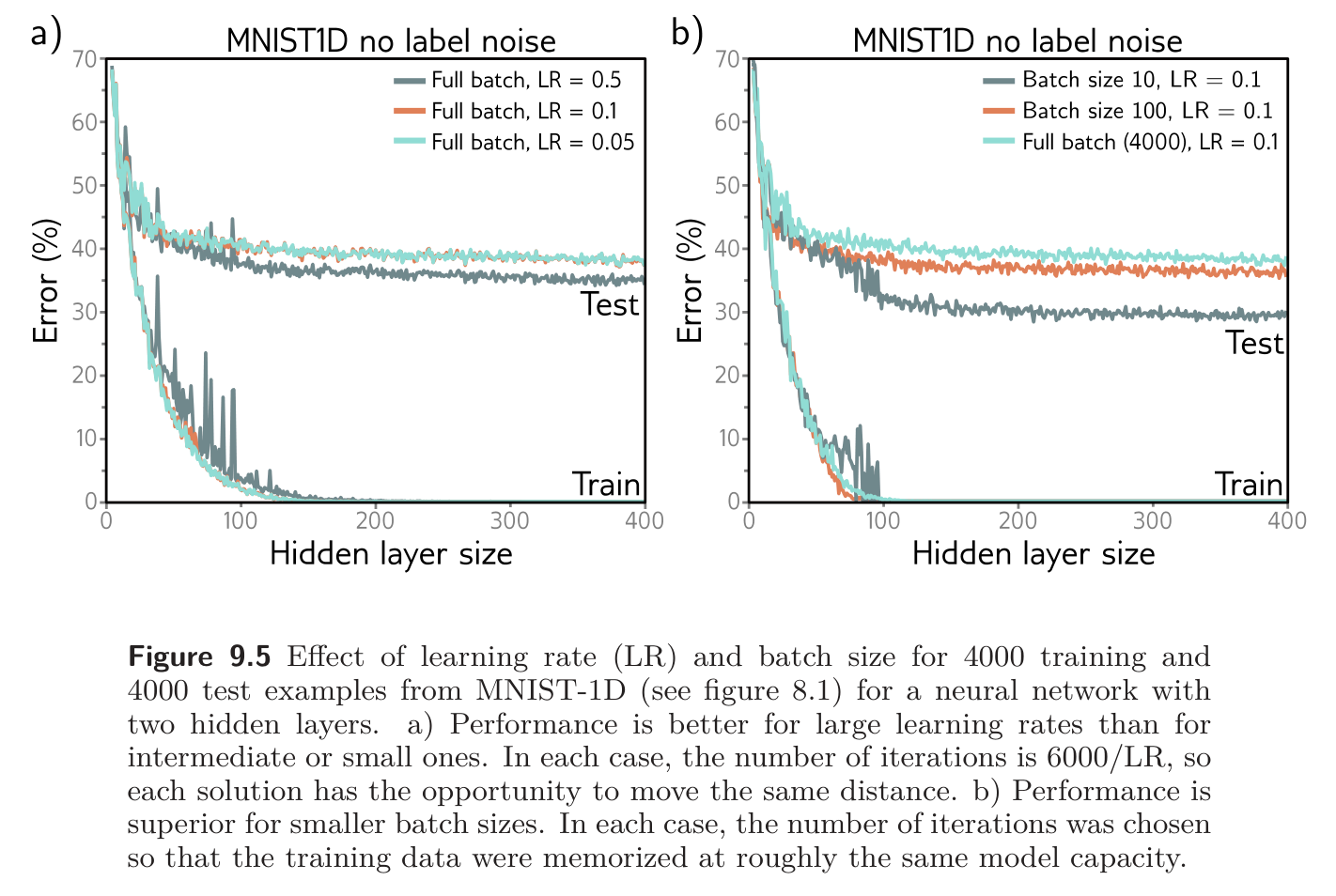
In other words, the discrete trajectory is repelled from places where the gradient norm is large (the surface is steep). This doesn’t change the position of the minima, where the gradients are zero anyway. However, it changes the effective loss function elsewhere and modifies the optimization trajectory, which potentially converges to a different minimum. Implicit regularization due to gradient descent may be responsible for the observation that full batch gradient descent generalizes better with larger step sizes (see fig 9.5a).

Implicit regularization in SGD

A similar analysis can be applied to SGD; now we seek a modified loss function such that the continuous version reaches the same places as the average of the possible random SGD updates. This can be shown to be:

$$\begin{array}{rl}{\tilde{L}}_{SGD}[\varphi ]& ={\hat{L}}_{GD}[\varphi ]+\frac{\alpha }{4B}\sum _{b=1}^B\left|\right|\frac{\partial L_b}{\partial \varphi }-\frac{\partial L}{\partial \varphi }|{|}^2\\ & =L[\varphi ]+\frac{\alpha }{4}\left|\right|\frac{\partial L}{\partial \varphi }|{|}^2+\frac{\alpha }{4B}\sum _{b=1}^B||\frac{\partial L_b}{\partial \varphi }-\frac{\partial L}{\partial \varphi }|{|}^2\end{array}$$

Here, $L_b$ is the loss for the $b$-th of the $B$ batches in an epoch. Specifically, $L$ now represents the means of the $I$ individual losses in the full dataset, while $L_b$ represents the mean of the $|\mathcal{B}|$ individual losses in a batch:

$$\begin{array}{r}L=\frac{1}{I}\sum _{i=1}^I{\ell }_i[{\mathbf{x}}_i,y_i]\text{and}{L}_b=\frac{1}{|\mathcal{B}|}\sum _{i\in {\mathcal{B}}_b}{\ell }_i[{\mathbf{x}}_i,y_i]\end{array}$$

Our equation above for ${\tilde{L}}_{SGD}[\varphi ]$ revealed an extra regularization term corresponding to the variance of the gradients of the batch losses $L_b$. In other words, SGD implicitly favors places where the gradients are stable (all the batches agree on the slope). This modifies the trajectory of the optimization process but does not necessarily change the position of the global minimum; if the model is over-parameterized, then it may fit all the training data exactly, so each of these gradient terms will be zero at the global minimum.

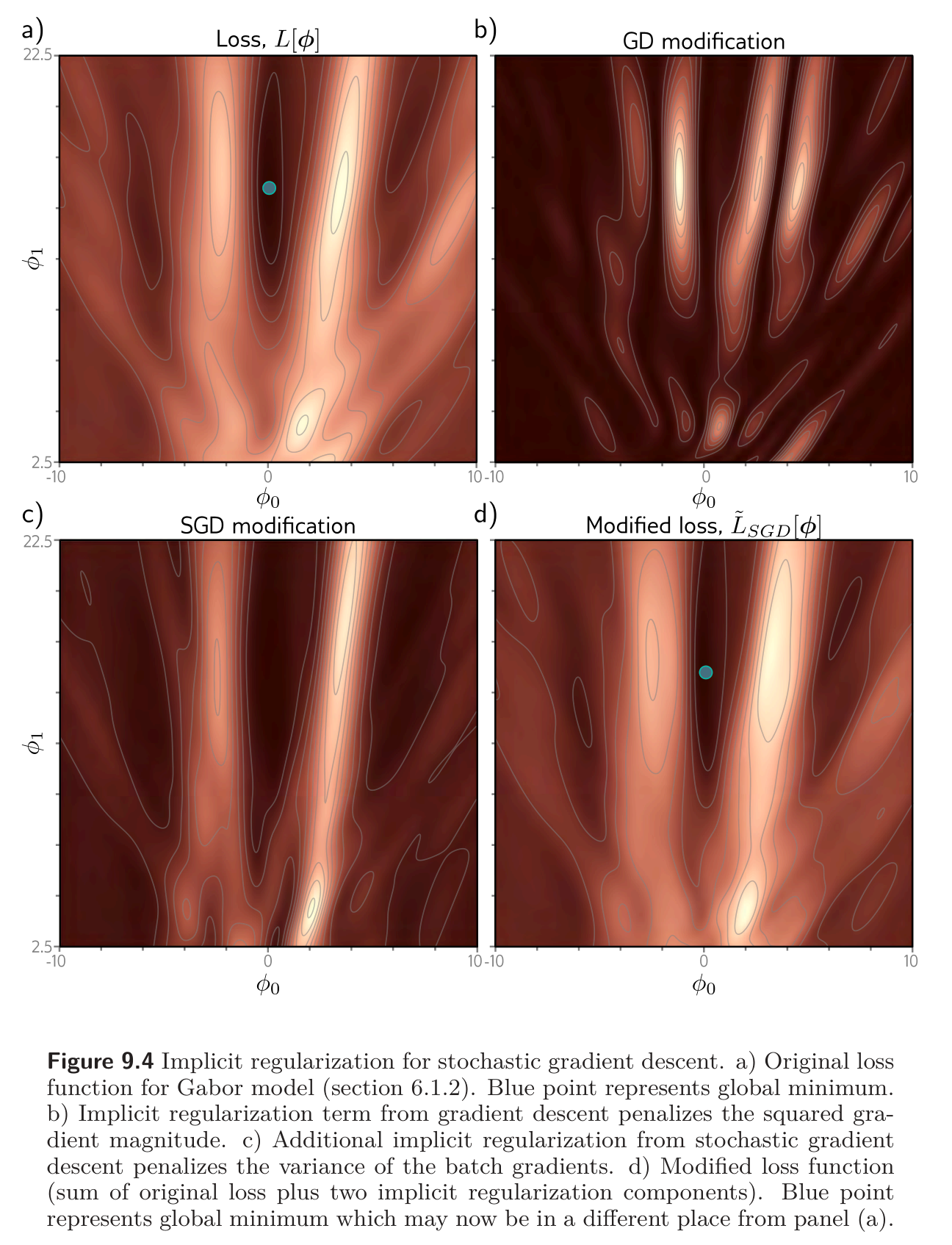
SGD generalizes better than gradient descent, and smaller batch sizes generally perform better than larger ones. One possible explanation is that the inherent randomness allows the algorithm to reached different parts of the loss function. However, it’s also possible that some or all of this performance increase is due to implicit regularization, as it encourages solutions where all the data fits well (so the batch variance is small) rather than solutions where some of the data fits extremely well and other data less well (perhaps with same overall loss but larger batch variance). The former solutions are likely to generalize better.