Heteroscedastic Regression

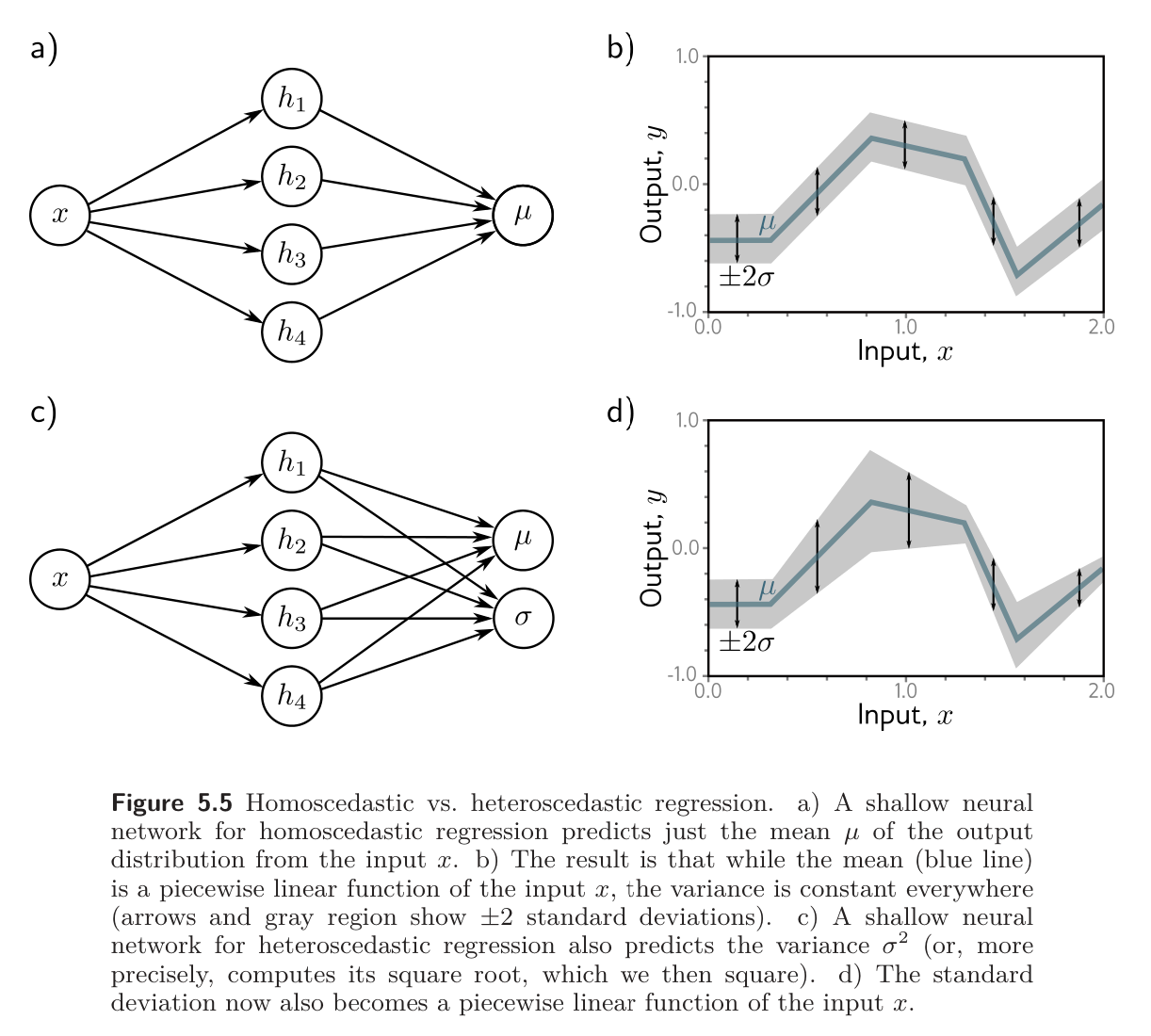
In simple univariate regression, we usually assume that the variance of the data is constant everywhere. However, this might be unrealistic. When the uncertainty of the model varies as a function of the input data, this is called heteroscedastic.

A simple way to model this is to train a neural network $\mathbf{f}[\mathbf{x},\varphi ]$ that computes both the mean and the variance.

• Example: Consider a shallow network with 2 outputs. We denote the first output as $f_1[\mathbf{x},\varphi ]$ and use this to predict the mean. We denote the second as $f_2[\mathbf{x},\varphi ]$ and use it to predict the variance.

Note that the variance must be positive, but we can’t guarantee that the network will produce a positive output. To ensure that the computed variance is positive, we pass the second network output through a function that maps an arbitrary value to a positive one. A suitable choice is the squaring function, giving

$$\begin{array}{rl}\mu & =f_1[\mathbf{x},\varphi ]\\ {\sigma }^2& =f_2[\mathbf{x},\varphi {]}^2\end{array}$$

which results in the loss function

$$\hat{\varphi }=\underset{\varphi }{\mathrm{argmin}}\left[-\sum _{i=1}^I\left(\log \left[\frac{1}{\sqrt{2\pi f_2[{\mathbf{x}}_i,\varphi {]}^2}}\right]-\frac{(y_i-f_1[{\mathbf{x}}_i,\varphi {]}^2)}{2f_2[{\mathbf{x}}_i,\varphi {]}^2}\right)\right]$$

when using the same maximum likelihood criterion approach that we used for univariate regression.