Gaussian Splatting

This is an overview of Gaussian Splatting, condensing the keypoints of the paper and including some implementation snippets from the original author’s implementation:

Paper
Repo

Motivation / Overview

Radiance field methods require neural network training, which is costly and render, while faster methods trade off speed for quality.

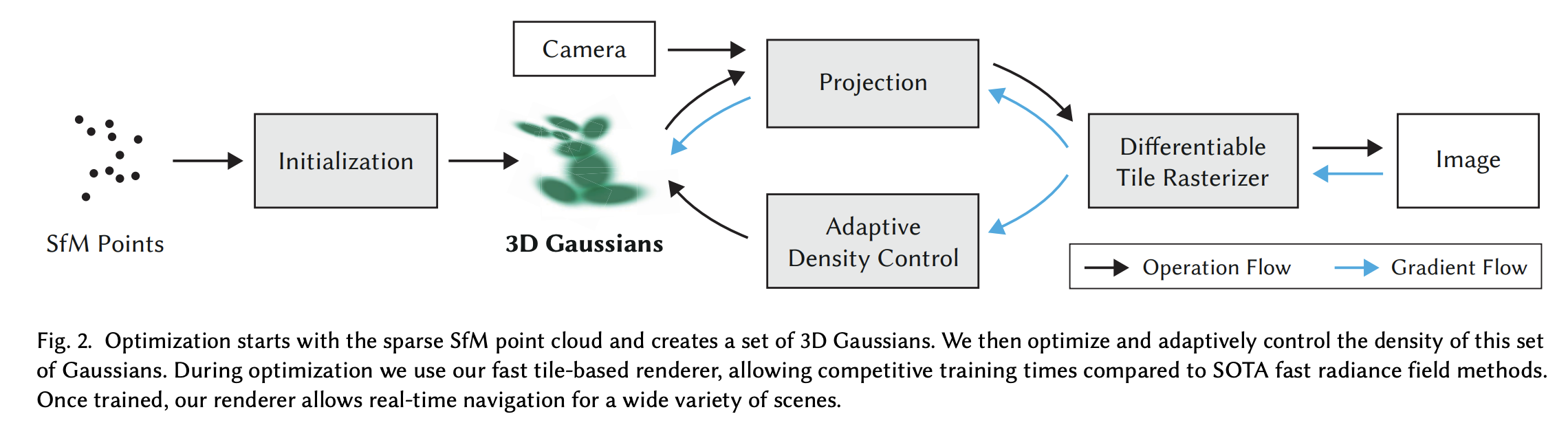
Three elements allows SOTA visual quality while maintaining competitive training times, and importantly allow high-quality real-time ( $\geq$ 30 fps) novel-view synthesis at 1080p resolution:

Scene representation with 3D Gaussians
Interleaved optimization/density control of the 3D Gaussians (optimizing anisotropic covariance)
Fast GPU algorithms for rendering.

Input

The input to the Gaussian Splatting method is a set of images of a static scene, together with the corresponding cameras calibrated by SfM, which produces a sparse point cloud.

3D Gaussians

Gaussian Representation

From the SfM points, a set of 3D Gaussians is produced. Each Gaussian is defined by a position (mean), covariance matrix, and opacity $α$ .

Specifically, each Gaussian is defined by a full 3D covariance matrix $Σ$ defined in world space at point (mean) $μ$ :

G (x) = e^{- \frac{1}{2} (x)^{T} Σ^{- 1} (x)}

This Gaussian is multiplied by $α$ in our blending process. It’s implemented in their repo as part of the rasterization submodule:

// diff-gaussian-rasterization/cuda-rasterizer/backward.cu
 
const float2 d = { xy.x - pixf.x, xy.y - pixf.y };
const float4 con_o = collected_conic_opacity[j];
const float power = -0.5f * (con_o.x * d.x * d.x + con_o.z * d.y * d.y) - con_o.y * d.x * d.y;
 
if (power > 0.0f)
	continue;
 
const float G = exp(power);
const float alpha = min(0.99f, con_o.w * G);
 
if (alpha < 1.0f / 255.0f)
	continue;

Covariance Matrix Representation

The covariance of 3D Gaussians must be represented in a way that can be optimized. (The purpose of this optimization is to adjust the shape, orientation, and size of the Gaussians so that they accurately represent the radiance field in 3D space.)

An obvious approach would be to directly optimize the covariance matrix $Σ$ to obtain 3D Gaussians that represent the radiance field. However, covariance matrices have physical meaning only when they are positive semi-definite. For optimization of parameters, gradient descent is used, which cannot be easily constrained to produce positive semi-definite matrices, and update steps and gradients can very easily create invalid covariance matrices.

Thus, a more intuitive expression is used for covariance, such that it can be optimized. The covariance matrix $Σ$ of a 3D Gaussian is analogous to describing the configuration of an ellipsoid. Given a scaling matrix $S$ and a rotation matrix $R$ , we can find the corresponding $Σ$ :

Σ = RS S^{T} R^{T}

To allow independent optimization of both factors, we store them separately: a 3D vector 𝑠 for scaling and a quaternion 𝑞 to represent rotation. These can be trivially converted to their respective matrices and combined, making sure to normalize 𝑞 to obtain a valid unit quaternion.

The implementation of this is shown below, also as part of the rasterization submodule.

// diff-gaussian-rasterization/cuda-rasterizer/forward.cu
 
// Forward method for converting scale and rotation properties of each
// Gaussian to a 3D covariance matrix in world space. Also takes care
// of quaternion normalization.
 
__device__ void computeCov3D(const glm::vec3 scale, float mod, const glm::vec4 rot, float* cov3D)
{
 
	// Create scaling matrix
	glm::mat3 S = glm::mat3(1.0f);
	S[0][0] = mod * scale.x;
	S[1][1] = mod * scale.y;
	S[2][2] = mod * scale.z;
	
	// Normalize quaternion to get valid rotation
	glm::vec4 q = rot;// / glm::length(rot);
	float r = q.x;
	float x = q.y;
	float y = q.z;
	float z = q.w;
	
	// Compute rotation matrix from quaternion
	glm::mat3 R = glm::mat3(
		1.f - 2.f * (y * y + z * z), 2.f * (x * y - r * z), 2.f * (x * z + r * y),
		2.f * (x * y + r * z), 1.f - 2.f * (x * x + z * z), 2.f * (y * z - r * x),
		2.f * (x * z - r * y), 2.f * (y * z + r * x), 1.f - 2.f * (x * x + y * y)
	);
	
	glm::mat3 M = S * R;
	
	// Compute 3D world covariance matrix Sigma
	glm::mat3 Sigma = glm::transpose(M) * M;
	
	// Covariance is symmetric, only store upper right
	cov3D[0] = Sigma[0][0];
	cov3D[1] = Sigma[0][1];
	cov3D[2] = Sigma[0][2];
	cov3D[3] = Sigma[1][1];
	cov3D[4] = Sigma[1][2];
	cov3D[5] = Sigma[2][2];
}

Projection to 2D

The 3D Gaussians must be projected to 2D for rendering. Given a viewing transformation $W$ , the covariance matrix $Σ^{'}$ in camera coordinates is given as follows:

Σ^{'} = J W Σ W^{T} J^{T}

where $J$ is the Jacobian of the affine approximation of the projective transformation.

This is done in the computeCov2D function of diff-gaussian-rasterization/cuda-rasterizer/forward.cu.

Anisotropy

A key point made throughout the paper is that this covariance is anisotropic – this allows the Gaussian to have different spreads in different directions, resulting in an ellipsoid shape rather than a sphere. The orientation and lengths of the ellipsoid’s axes are determined by the covariance matrix. This allows for better scene representation as we are not restricted representing symmetric features, which would be the isotropic case.

Optimization and Density Control of Gaussians

The optimization step creates a dense set of 3D Gaussians accurately representing the scene for free-view synthesis. In addition to positions $p$ , $α$ , and covariance $Σ$ , spherical harmonic (SH) coefficients are also optimized, representing color $c$ of each Gaussian to correctly capture the view-dependent appearance of the scene. The optimization of these parameters is interleaved with steps that control the density of the Gaussians to better represent the scene.

The optimization is based on successive iterations of rendering and comparing the resulting image to the training views in the captured dataset. Inevitably, geometry may be incorrectly placed due to the ambiguities of 3D to 2D projection. Thus, the optimization needs to be able to create, destroy, and move geometry if it has been incorrectly positioned.

SGD is used for optimization.

Setup

A sigmoid activation function is used for opacity $α$ to constraint it in the 0-1 range and obtain smooth gradients.
An exponential activation function for the scale of the covariance for similar reasons.
The initial covariance matrix is estimated as an isotropic Gaussian with axes equal to the mean of the distance to the closest three points

# scene/GaussianModel.py
 
class GaussianModel:
 
	def setup_functions(self):
		def build_covariance_from_scaling_rotation(scaling, scaling_modifier, rotation):
		L = build_scaling_rotation(scaling_modifier * scaling, rotation)
		actual_covariance = L @ L.transpose(1, 2)
		symm = strip_symmetric(actual_covariance)
		return symm
 
	self.scaling_activation = torch.exp
	self.scaling_inverse_activation = torch.log
	
	self.covariance_activation = build_covariance_from_scaling_rotation
	
	self.opacity_activation = torch.sigmoid
	self.inverse_opacity_activation = inverse_sigmoid
	
	self.rotation_activation = torch.nn.functional.normalize

Loss

A standard exponential decay scheduling technique is used. The loss function is $L_{1}$ combined with a D-SSIM term:

L = (1 - λ) L_{1} + λ L_{D-SSIM}

Implementation:

train.py:

# Loss
gt_image = viewpoint_cam.original_image.cuda()
Ll1 = l1_loss(image, gt_image)
loss = (1.0 - opt.lambda_dssim) * Ll1 + opt.lambda_dssim * (1.0 - ssim(image, gt_image))
loss.backward()

loss_utils.py:

def l1_loss(network_output, gt):
	return torch.abs((network_output - gt)).mean()
 
def ssim(img1, img2, window_size=11, size_average=True):
	channel = img1.size(-3)
	window = create_window(window_size, channel)
 
if img1.is_cuda:
	window = window.cuda(img1.get_device())
	window = window.type_as(img1)
 
	return _ssim(img1, img2, window, window_size, channel, size_average)

Densification

Initially, the method starts with a set of sparse points from SfM, but densification is done to adaptively control the number of Gaussians and their density over unit volume. This allows us to go from an initial sparse set of Gaussians to a denser set that better represents the scene, and with correct parameters.

During training, densification is done every 100 iterations (after optimization warm-up).

There are two cases where densification needs to be done:

Under-Reconstruction: Regions with missing geometric features. In this case, small Gaussians in the space are cloned and moved in the direction of the positional gradient.
Over-Reconstruction: Regions where Gaussians cover large areas in a scene. Here, large Gaussians in regions with high variance need to be split into smaller Gaussians.

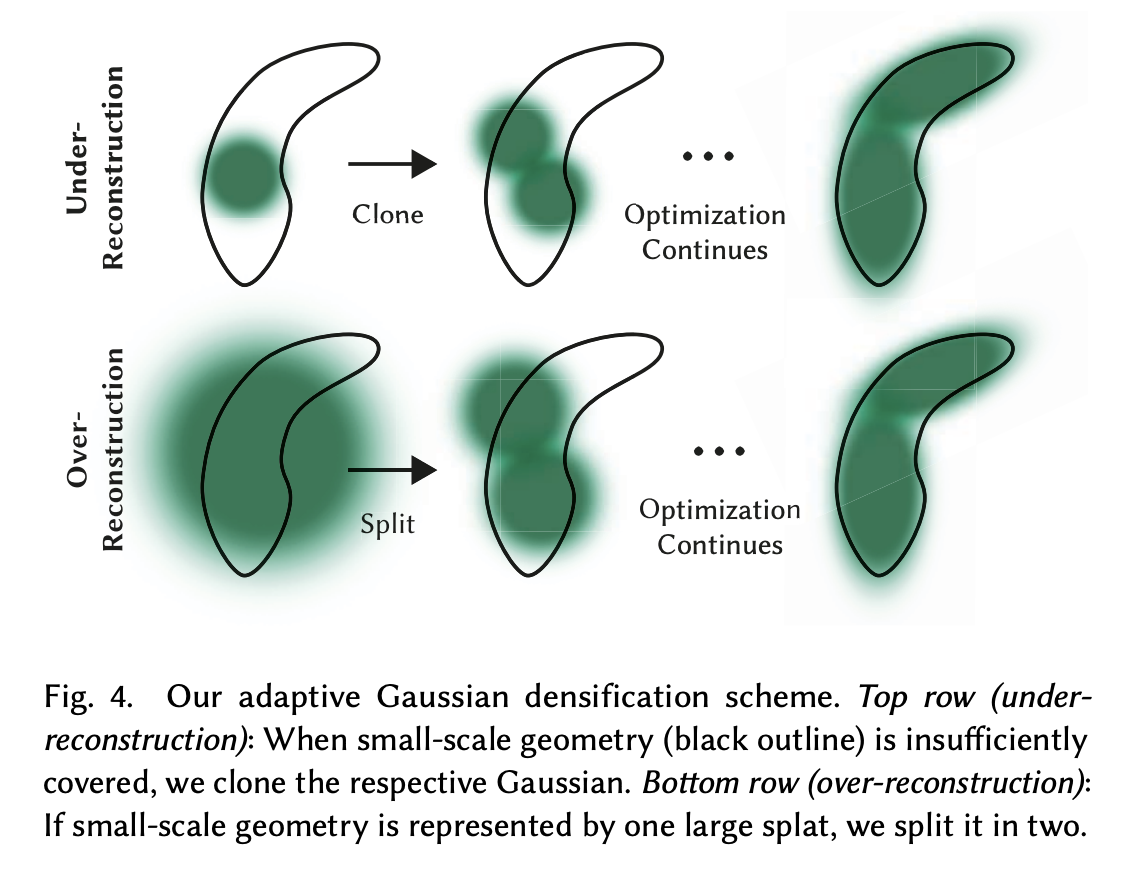
Also, Gaussians that are essentially transparent, i.e., with less than a threshold $ϵ_{α}$ , are removed.

Implementation:

def densify_and_split(self, grads, grad_threshold, scene_extent, N=2):
 
	n_init_points = self.get_xyz.shape[0]
	
	# Extract points that satisfy the gradient condition
	padded_grad = torch.zeros((n_init_points), device="cuda")
	padded_grad[:grads.shape[0]] = grads.squeeze()
	selected_pts_mask = torch.where(padded_grad >= grad_threshold, True, False)
	selected_pts_mask = torch.logical_and(selected_pts_mask,
	torch.max(self.get_scaling, dim=1).values > self.percent_dense*scene_extent)
	
	stds = self.get_scaling[selected_pts_mask].repeat(N,1)
	means =torch.zeros((stds.size(0), 3),device="cuda")
	samples = torch.normal(mean=means, std=stds)
	rots = build_rotation(self._rotation[selected_pts_mask]).repeat(N,1,1)
	new_xyz = torch.bmm(rots, samples.unsqueeze(-1)).squeeze(-1) + self.get_xyz[selected_pts_mask].repeat(N, 1)
	new_scaling = self.scaling_inverse_activation(self.get_scaling[selected_pts_mask].repeat(N,1) / (0.8*N))
	new_rotation = self._rotation[selected_pts_mask].repeat(N,1)
	new_features_dc = self._features_dc[selected_pts_mask].repeat(N,1,1)
	new_features_rest = self._features_rest[selected_pts_mask].repeat(N,1,1)
	new_opacity = self._opacity[selected_pts_mask].repeat(N,1)
	
	self.densification_postfix(new_xyz, new_features_dc, new_features_rest, new_opacity, new_scaling, new_rotation)
	
	prune_filter = torch.cat((selected_pts_mask, torch.zeros(N * selected_pts_mask.sum(), device="cuda", dtype=bool)))
	self.prune_points(prune_filter)
 
  
 
def densify_and_clone(self, grads, grad_threshold, scene_extent):
 
	# Extract points that satisfy the gradient condition
	
	selected_pts_mask = torch.where(torch.norm(grads, dim=-1) >= grad_threshold, True, False)
	selected_pts_mask = torch.logical_and(selected_pts_mask,
	torch.max(self.get_scaling, dim=1).values <= self.percent_dense*scene_extent)
	new_xyz = self._xyz[selected_pts_mask]
	new_features_dc = self._features_dc[selected_pts_mask]
	new_features_rest = self._features_rest[selected_pts_mask]
	new_opacities = self._opacity[selected_pts_mask]
	new_scaling = self._scaling[selected_pts_mask]
	new_rotation = self._rotation[selected_pts_mask]
	
	self.densification_postfix(new_xyz, new_features_dc, new_features_rest, new_opacities, new_scaling, new_rotation)
 
def densify_and_prune(self, max_grad, min_opacity, extent, max_screen_size):
 
	grads = self.xyz_gradient_accum / self.denom
	grads[grads.isnan()] = 0.0
	
	self.densify_and_clone(grads, max_grad, extent)
	self.densify_and_split(grads, max_grad, extent)
	
	prune_mask = (self.get_opacity < min_opacity).squeeze()
	if max_screen_size:
		big_points_vs = self.max_radii2D > max_screen_size
		big_points_ws = self.get_scaling.max(dim=1).values > 0.1 * extent
		prune_mask = torch.logical_or(torch.logical_or(prune_mask, big_points_vs), big_points_ws)
	self.prune_points(prune_mask)
	
	torch.cuda.empty_cache()

An effective way to moderate the increase in the number of Gaussians is to set the value close to zero every $N = 3000$ . The optimization then increases the $α$ for the Gaussians where this is needed, while allowing our culling approach to remove Gaussians with $α$ less than $ϵ_{α}$ as described above.

Fast Differentiable Rasterization

Essentially the authors create a fast tile-based rasterizer for Gaussian splats. The exact methods behind this don’t seem very relevant for our use-case. The code is contained in the diff-gaussian-rasterization submodule.

/notes/

Recent

LADR Exercises 2A

Linear Independence

Linear Dependence Lemma