Matrix Representation of Linear Map

Suppose $T\in \mathcal{L}(V,W)$ and $v_1,\dots ,v_n$ is a basis of $V$ and $w_1,\dots ,w_m$ is a basis of $W$.

The matrix of $T$ with respect to these bases is the $m$-by-$n$ matrix $\mathcal{M}(T)$ whose entries are defined by

$$T{v}_k=A_{1,k}{w}_1+\cdots +A_{m,k}{w}_m$$

• If the bases $v_1,\dots ,v_n$ and $w_1,\dots ,w_m$ are not clear from the context, then the notation $\mathcal{M}(T,(v_1,\dots ,v_n),(w_1,\dots ,w_m))$ is used.

The matrix of a linear map depends on the bases of $V$ and $W$, as well as on $T$.

To remember how $\mathcal{M}(T)$ is constructed from $T$, we can write:

• The basis vectors $v_1,\dots ,v_m$ across the top of the matrix for the domain
• The basis vectors $w_1,\dots ,w_m$ along the left of the matrix for the space into which $T$ maps

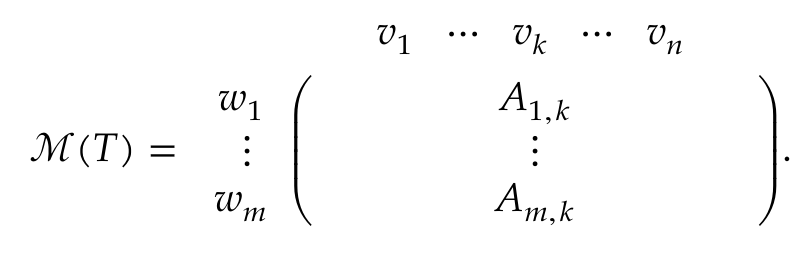
• In the matrix above, only the $k$-th column is shown. Thus, the second index of each displayed entry is $k$.

This reminds us that $T{v}_k$ can be computed from $\mathcal{M}(T)$ by multiplying each entry in the $k$-th column by the corresponding $w_j$ from the left column, and then adding up the resulting vectors. Or, the $k$-th column of $\mathcal{M}(T)$ consists of the scalars required to write $T{v}_k$ as a combination of $w_1,\dots ,w_m$:

$$T{v}_k=\sum _{j=1}^m{A}_{j,k}{w}_j$$

Clarifying example

For example, if we have $T:{\mathbb{F}}^3\to {\mathbb{F}}^2$:

\begin{align} & \begin{matrix} v_{1} & v_{2} & v_{3} \end{matrix} \\[2ex] \begin{matrix} w_{1} \\ w_{2}

\end{matrix},,,,

& \begin{bmatrix} 1 & 2 & 0 \ 0 & 3 & 4 \end{bmatrix} \end{align}

Then we can calculate $Tv_{1}$ as $1w_{1}+0w_{2}$, $Tv_{2}$ as $2w_{1}+3w_{2}$, and $Tv_{3}=0w_{1}+4w_{2}$.

If $T$ is a linear map from ${\mathbb{F}}^n$ to ${\mathbb{F}}^m$, then we can generally assume the bases in questions are the standard ones ($k$-th basis vector is $1$ in the $k$-th slot and $0$ in all other slots). If we think of the elements of ${\mathbb{F}}^m$ as columns of $m$ numbers, we can think of the $k$-th column of $\mathcal{M}(T)$ as $T$ applied to the $k$-th standard basis vector.

Examples

Example: Matrix of Linear Map from ${\mathbb{F}}^2$ to ${\mathbb{F}}^3$

Suppose $T\in \mathcal{L}({\mathbb{F}}^2,{\mathbb{F}}^3)$ is defined by

$$T(x,y)=(x+3y,2x+5y,7x+9y)$$

We can check the results of the bases of ${\mathbb{F}}^2$:

• $T(1,0)=(1,2,7)$
• $T(0,1)=(3,5,9)$

Then, the matrix of $T$ with respect to the standard bases is the $3\times 2$ matrix:

$$\mathcal{M}(T)=\left(\begin{array}{cc}1& 3\\ 2& 5\\ 7& 9\end{array}\right)$$

Example: Matrix of Differentiation Map from ${\mathcal{P}}_3(\mathbb{R})$ to ${\mathcal{P}}_2(\mathbb{R})$:

Suppose $D\in \mathcal{L}(P_3(\mathbb{R}),P_2(\mathbb{R}))$ is the differentiation map defined by $Dp=p^{\prime }$. Because $(x^n{)}^{\prime }=n{x}^{n-1}$, the matrix of $D$ with respect to the standard bases is:

$$\mathcal{M}(D)=\left(\begin{array}{cccc}0& 1& 0& 0\\ 0& 0& 2& 0\\ 0& 0& 0& 3\end{array}\right)$$

We can see that each column is just differentiation applied to each basis element in $\{1,x,x^2,x^3\}$ .