Geometry of Linear Equations

The fundamental problem of linear algebra:

$$n\text{ linear equations},n\text{ unknowns}$$

Let’s use the example:

$$\begin{array}{r}2x-y=0\\ -x+2y=3\end{array}$$

Or in a matrix:

$$\underset{A}{\underbrace{\left[\begin{array}{cc}2& -1\\ -1& 2\end{array}\right]}}\underset{x}{\underbrace{\left[\begin{array}{c}x\\ y\end{array}\right]}}=\underset{b}{\underbrace{\left[\begin{array}{c}0\\ 3\end{array}\right]}}$$

---

Row picture

Row picture is considers the system one line at a time.

• What points fulfill the first equation $2x-y=0$?
• What points fulfill the second equation $-x+2y=3$? This can be effectively done by plotting the lines on a graph. Then, we just find the intersection: 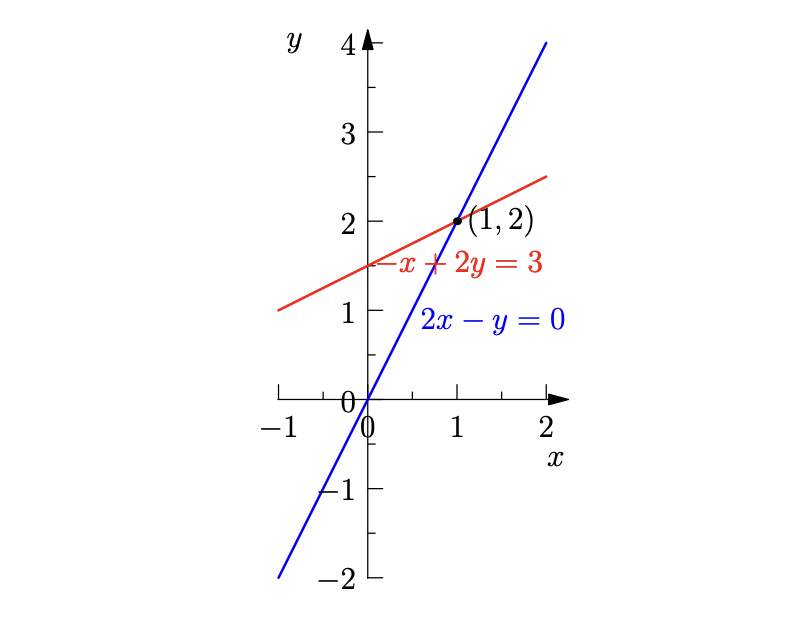Plugging the intersection point $(1,2)$ into the equations we see that:

$$\begin{array}{rl}2(1)-2& =0\\ -1+2(2)& =3\end{array}$$

---

Column picture

Column picture considers the system one column at a time by isolating each variable

$$x\left[\begin{array}{c}-2\\ 1\end{array}\right]+y\left[\begin{array}{c}-1\\ 2\end{array}\right]=\left[\begin{array}{c}0\\ 3\end{array}\right]$$

Here, we solve the equation by thinking in terms of linear combinations of vectors:

• We need to add $x$ copies of the first vector to $y$ copies of the 2nd vector to get $[0,3]$

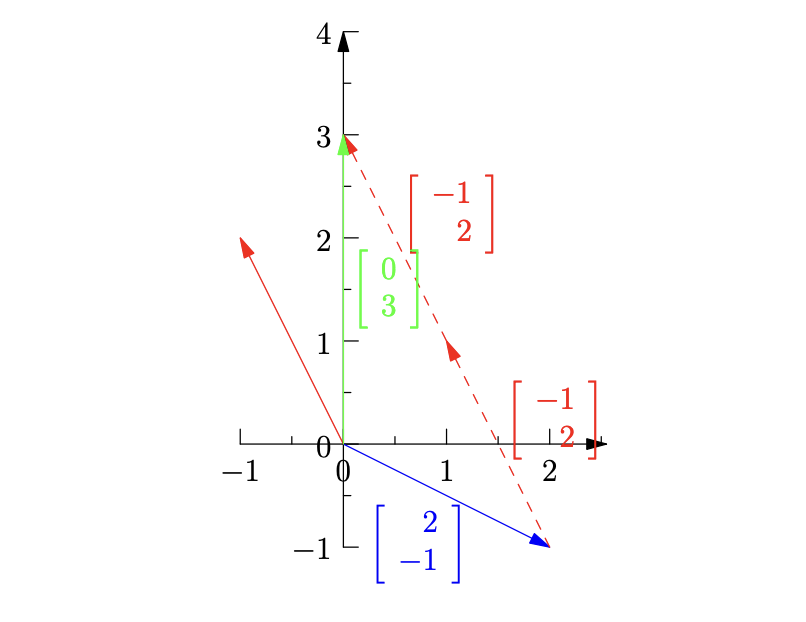
We find that having having $x=1$ and $y=2$ indeed gives us:

$$1\left[\begin{array}{c}2\\ -1\end{array}\right]+2\left[\begin{array}{c}-1\\ 2\end{array}\right]=\left[\begin{array}{c}2\\ -1\end{array}\right]+\left[\begin{array}{c}-2\\ 4\end{array}\right]=\left[\begin{array}{c}0\\ 3\end{array}\right]$$

---

Matrix form

We write the equations in a matrix:

$$\left[\begin{array}{cc}2& -1\\ -1& 2\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]\left[\begin{array}{c}0\\ 3\end{array}\right]$$

Here, the coefficient matrix $A$ is:

$$A=\left[\begin{array}{cc}2& -1\\ -1& 2\end{array}\right]$$

And the vector $x$ is the vector of unknowns:

$$x=\left[\begin{array}{c}x\\ y\end{array}\right]$$