Vector Equations of Lines

How do we use vector functions to describe lines?

• Vector function – take variable(s), return a vector.
  • Vector form
  • Parametric form
  • Parametric form

For example: $\vec{r}(t)=⟨t,1⟩$

• Describes a position vector $\vec{r}=⟨a,b⟩$ that starts at the origin and ends at $(a,b)$
• Some example inputs into the function:

$$r(3)=⟨-3,1⟩,r(-1)=⟨-1,1⟩,r(2)=⟨2,1⟩,r(5)=⟨5,1⟩$$

Thus, we can describe lines and shapes like:

---

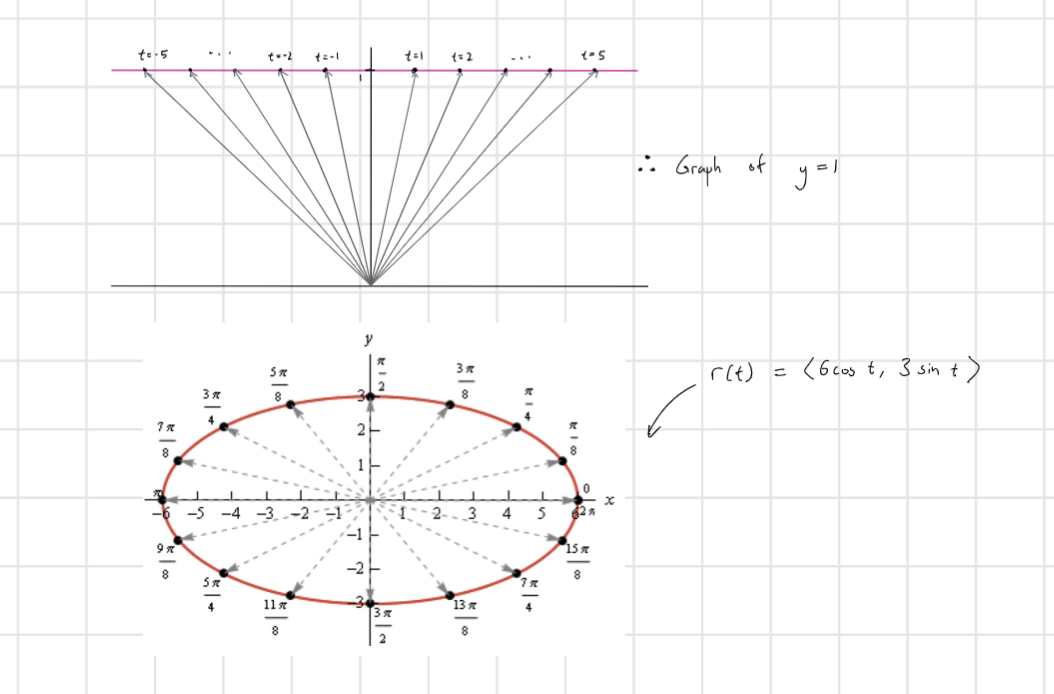
Vector form

Slope needs to be defined as a direction in 3D.

• Let $P_0=(x_0,y_0,z_0)$ and $P=(x,y,z)$
• Let $\vec{r}=⟨x_0,y_0,z_0⟩$ and $\vec{r}=⟨x,y,z⟩$
• Let $\vec{a}=\overrightarrow{P_{0}P}$
• Let $\vec{v}=⟨a,b,c⟩$ that is parallel to $\vec{a}$

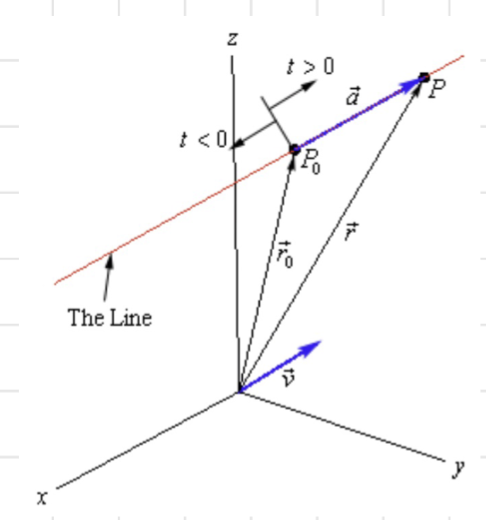
Then, we have $\vec{r}=\overrightarrow{r_0}+\vec{a}$, and there is some $t$ that $\vec{a}=t\vec{v}$. Thus, we have:

$$\boxed{\vec{r}=\overrightarrow{r_0}+t\vec{v}=⟨x_0,y_0,z_0⟩+t⟨a,b,c⟩}\text{\hspace{1em}(1)}$$

This is the vector form of equation of a line.

$t\vec{v}$ lies along the line and tells us how far from the original point we travel.

• For $t⟩0$, we move in the direction of $\vec{v}$
• For $t⟨0$, we move in the opposite direction

---

Parametric form

From equation $(1)$ above we can get:

$$⟨x,y,z⟩=⟨x_0+ta,y_0+tb,z_0+tc⟩$$

Thus, we can get a parametric form:

$$\boxed{\begin{array}{rl}x& =x_0+ta\\ y& =y_0+tb\\ z& =z_0+tc\end{array}}$$

---

Symmetric form

If we isolate $t$ in the parametric form, we can get:

$$\boxed{\frac{x-x_0}{a},\frac{y-y_0}{b},\frac{z-z_0}{c}}$$

This is still valid even if one of them is $0$:

• For example, if $b=0$, $t$ will not exist in the parametric equation for $y$and so we will only solve the parametric equations for $x$ and $z$ for $t$:

$$\frac{x-x_0}{a}=\frac{z-z_0}{c},y=y_0$$