Multivariable & Partial Chain Rule

Standard chain rule for $y=f(x)$ and $x=g(t)$:

$$\frac{dy}{dt}=\frac{dy}{dx}\frac{dx}{dt}$$

For a function with two variable, $z=f(x,y)$, there are two cases

Case 1:

Compute $\frac{dz}{dt}$ for $z=f(x,y),x=g(t),y=h(t)$.

This is analogous to the standard chain rule; we are going to compute an ordinary derivative since $z$ would be a function of $t$ is we substitute in for $x$ and $y$. The chain rule is:

$$\frac{dz}{dt}=\frac{\partial f}{\partial x}\frac{dx}{dt}+\frac{\partial f}{\partial y}\frac{dy}{dt}$$

Basically, we differentiate $f$ with respect to each variable in it and then multiply each of these by the derivative of that variable with respect to $t$, then add.

Special sub-case of Case 1:

$$z=f(x,y),y=g(x)$$

In this case the chain rule for $\frac{dz}{dt}$ becomes:

$$\begin{array}{rl}\frac{dz}{dx}& =\frac{\partial f}{\partial x}\frac{dx}{dx}+\frac{\partial f}{\partial y}\frac{dy}{dx}\\ & =\frac{\partial f}{\partial x}+\frac{\partial f}{\partial y}\frac{dy}{dx}\end{array}$$

Case 2:

Compute $\frac{\partial z}{\partial s}$ and $\frac{\partial z}{\partial t}$ for $z=f(x,y)$, $x=g(s,t)$, $y=h(s,t)$.

In this case if we were to substitute in for $x$ and $y$, we would get $z$ as a function of $s$ and $t$; this is why we have to compute partial derivatives here and that there are two of them.

Thus, we have:

$$\begin{array}{rl}\frac{\partial z}{\partial s}& =\frac{\partial f}{\partial x}\frac{\partial x}{\partial s}+\frac{\partial f}{\partial y}\frac{\partial y}{\partial s}\\ \frac{\partial z}{\partial t}& =\frac{\partial f}{\partial x}\frac{\partial x}{\partial t}+\frac{\partial f}{\partial y}\frac{\partial y}{\partial t}\end{array}$$

General Version of Chain Rule:

Suppose that $z$ is a function of $n$ variables, $x_1,x_2,\dots ,x_n$, and that each of these variables are in turn functions of $m$ variables, $t_1,t_2,\dots ,t_m$. Then for any variable $t_i$, $i=1,2,\dots ,m$, we have:

$$\frac{\partial z}{\partial t_i}=\frac{\partial z}{\partial x_1}\frac{\partial x_1}{\partial t_i}+\frac{\partial z}{\partial x_2}\frac{\partial x_2}{\partial t_i}+\cdots +\frac{\partial z}{\partial x_n}\frac{\partial x_n}{\partial t_i}$$

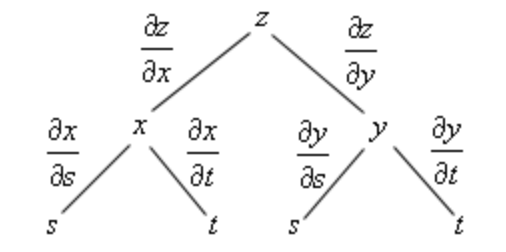
Basically, we want to find the partial derivative of the big function with respect to the sub-functions, and then take the partial derivative of the sub-functions with respect to their variables. In tree form, for $\frac{\partial z}{\partial s}$ given that $z=f(x,y)$, $x=g(s,t)$ , $y=h(s,t)$: