Limits (Multivariable)

Basic single-variable limit:

$$\underset{x\to a}{\lim }f(x)=L$$

if we have

$$\underset{x\to a^{+}}{\lim }f(x)=\underset{x\to a^{-}}{\lim }f(x)=L$$

Extending to multi-variable:

$$\underset{(x,y)\to (a,b)}{\lim }f(x,y)$$

In order for this to exist, the function must be approaching the same value. The problem here is that there are an infinite number of paths that we can take as we move toward $(a,b)$. How can we check infinite paths? The answer is continuity.

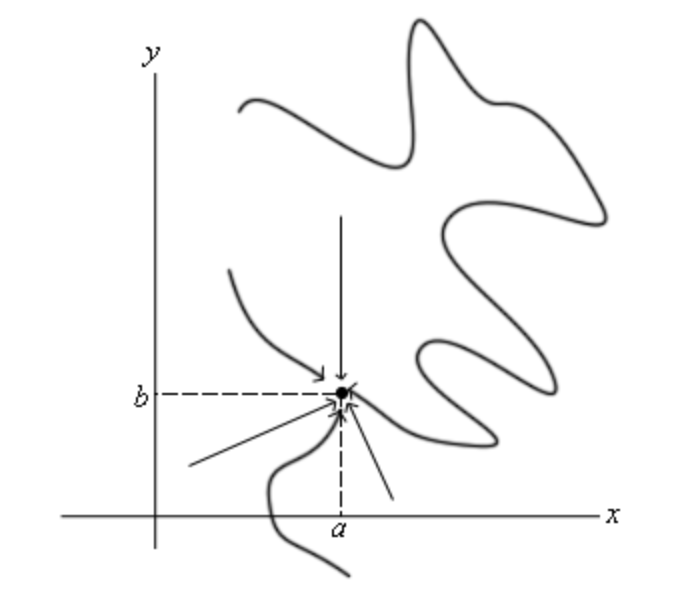
Definition: Continuity

A function $f(x,y)$ is continuous at the point $(a,b)$ if

$$\underset{(x,y)\to (a,b)}{\lim }f(x,y)=f(a,b)$$

Thus, if we know a function is continuous at a point then all we need to do to take the limit is to evaluate $f(a,b)$.