Interpretations of Partial Derivatives

Rates of change

• $f_x(x,y)$ represents the rate of change of the function $f(x,y)$ as we change $x$ and hold $y$

• $f_y(x,y)$ represents the rate of change of the function $f(x,y)$ as we change $y$ and hold $x$

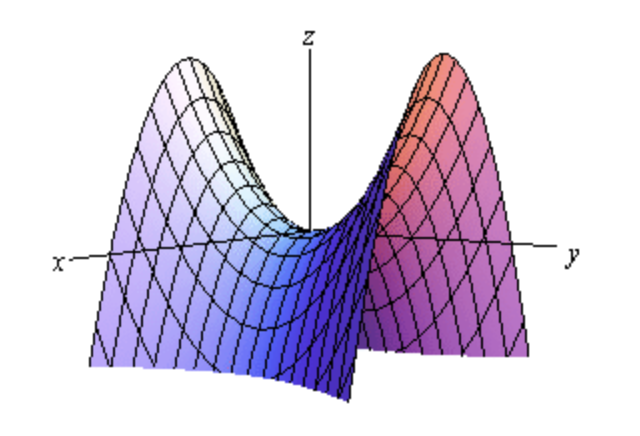  In the hyperbolic paraboloid above, we can see that if we move along the y-axis, the graph is increasing and if we move along the x-axis the graph is decreasing

Slopes of tangent:

Partial derivatives are the slopes of traces:

• The partial derivative of $f_x(a,b)$ is the slope of the trace of $f(x,y)$ for the plane $y=b$ at the point $(a,b)$.
• The partial derivative of $f_y(a,b)$ is the slope of the trace of $f(x,y)$ for the plane $x=a$ at the point $(a,b)$

Getting the equations of tangent line

The point is easy to find by plugging the points into the equation:

$$(a,b,f(a,b))$$

The parallel (or tangent) vector is then:

$$\vec{r}(x,y)=⟨x,y,z⟩=⟨x,y,f(x,y)⟩$$

If we differentiate with respect to $x$ we will get a tangent vector to traces for the plane $y=b$ (i.e. for fixed $y$):

$$\begin{array}{rl}{\vec{r}}_x(x,y)& =⟨1,0,f_x(x,y)⟩\\ \vec{r}(t)& =⟨a,b,f(a,b)⟩+t⟨1,0,f_x(a,b)⟩\end{array}$$

For traces with fixed $x$ such that $x=a$:

$$\begin{array}{rl}{\vec{r}}_y(x,y)& =⟨0,1,f_y(x,y)⟩\\ \vec{r}(t)& =⟨a,b,f(a,b)⟩+t⟨0,1,f_y(a,b)⟩\end{array}$$