Ternary Tree Paths

Given a ternary tree (each node of the tree has at most three children), find all root-to-leaf paths.

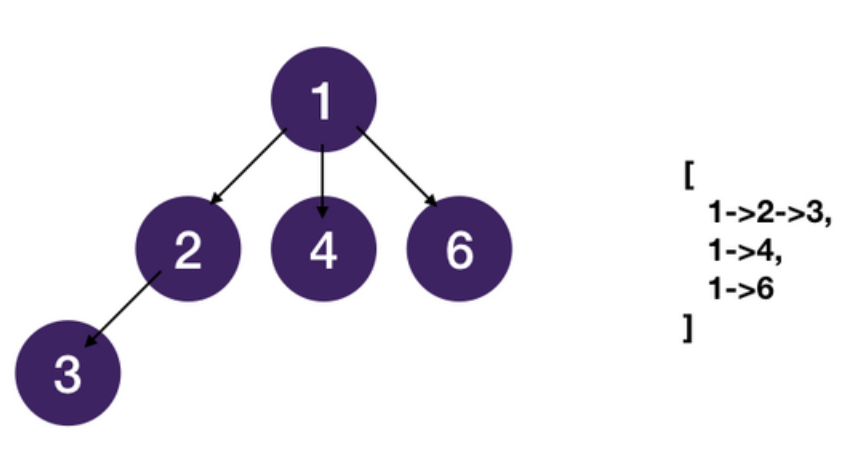
Solution

This is a DFS problem where we want to track a state; in this case, the state is path, which we use to keep track of the nodes we have visited to reach the current node and use it to construct our solution when we reach leaf nodes.

def ternary_tree_paths(root: Node) -> List[str]:
    
    def dfs(node, path, result):
        if all (children is None for children in node.children):
            result.append('->'.join(path) + '->' + str(node.val))
            return
                          
        for child in node.children:
            if child is not None:
                dfs(child, path + [str(node.val)], result)
                          
    
    result = []
    if root: dfs(root, [], result)
                         
    return result

Base case: If a node is a leaf (no children), join the values in path with ->, add the current node value to the end, and append this all to the result.

Recursive case: Iterates through each child of the current node; if it exists, call dfs on it. Here we pass the current path plus the current node value and the result list, so we can accumulate paths.

Alternate Solution

In the recursive call in the previous solution, we create a new list each time we recurse with path + [root.val]. This is not space-efficient because creating a new list requires allocating new space in memory and copying over each element. A more efficient way is to use a single list path and push and pop following the call stack. Remember that path is a list so we can push with .append() and pop with .pop().

for child in node.children:
	if child is not None:
		path.append(str(root.val))
		dfs(child, path, result)
		path.pop()