Tolerances and Fits

Tolerance: Permissible deviation of a dimension from the specified basic size

Fit: The relative looseness (clearance) or tightness (interference) of mating parts

• Clearance fit: A fit that allows free motion between two parts to be mated (loose, running or sliding fit).
  • $\text{Min hole diameter}<\text{Max shaft diameter}$
• Interference fit: A fit that requires two parts to be forced together, often with a press machine (tight fit)
  • $\text{Max hole diameter}<\text{Min shaft diameter}$
• Transition fit: A fit requiring light force to (dis)assemble
  • Both clearance and interference are possible within the specified tolerance

Methods for Engineering Tolerance

• Blanket tolerance: The basic size in drawing implies a certain tolerance.
  • For example, $2.5$ implies $2.5\pm 0.25\text{ mm}$, $2.500$ means $2.5\pm 0.012\text{ mm}$

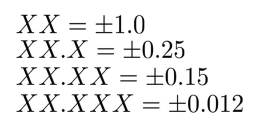
• Unidirectional or bidirectional tolerance

  • $1.5\pm 0.01$ (bidirectional)
  • $1.5_{0.00}^{+0.01}$

• International Tolerance (IT) grade, e.g. H7/g6

  • A system of standard tolerance (ISO 286)
  • Divided into two categories: hole and shaft
  • Labeled with a letter (upper case for hole, lower for shaft) and a number (grade number)

Fundamental Deviation

Fundamental deviation defines the position of the tolerance zone relative to the nominal or basic size. It determines whether the tolerance zone lies above (positive deviation), below (negative deviation), or straddles the nominal size.

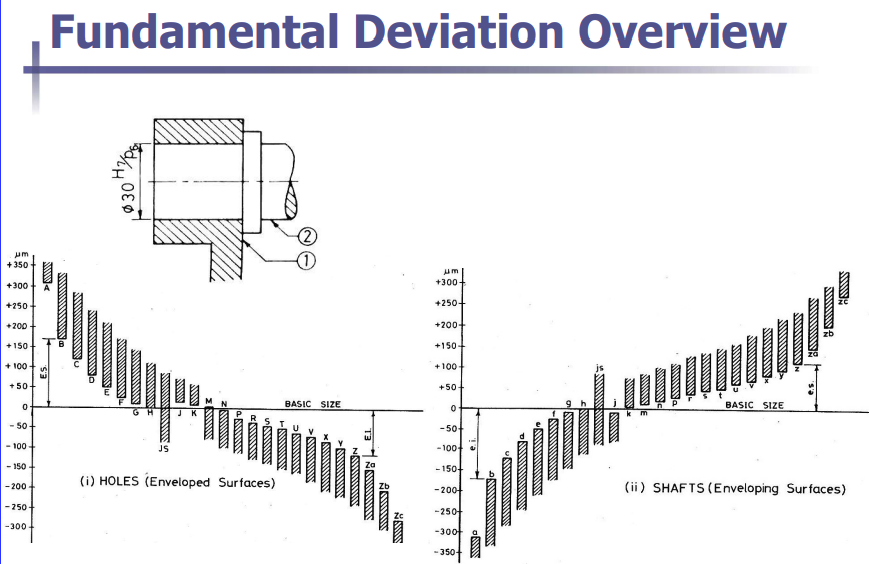
Holes (left diagram):

• The horizontal axis represents the specific tolerance grade (e.g., H, G, etc.)
• Each letter represents a specific tolerance grade (H, G, etc)
• Fundamental deviation for holes can either be positive (above basic size) or negative (below the basic size).
• For example
  • H has a deviation that starts exactly at the basic size (no negative deviation).
  • D, E, F have positive deviations.
  • G, H, K are closer to the basic size but still allow for positive deviation.

Shafts (right diagram):

• Same concept as previous
• For example:
  • h has no positive deviation
  • g, f, e have negative deviations

Example

Bearings Example 7

Determine the actual dimension and fitting type:

1. $\varphi$ 300 H7/m6
2. $\varphi$ 120 G8/f7
3. $\varphi$ 35 H7/r6

1. We have:

$$\begin{array}{r}\varphi 300\text{ H}7\equiv \varphi 300_{0.000}^{+0.052}\\ \varphi 300\text{ m}6\equiv \varphi 300_{0.020}^{+0.052}\end{array}$$

There is some potential inference, so this is a transition fit.

2. We have

$$\begin{array}{rl}\varphi 120\text{ G}8& \equiv \varphi 120_{0.012}^{+0.076}\\ \varphi 120\text{ f}7& \equiv \varphi 120_{-0.071}^{-0.036}\\ \text{Minimum clearance}& =0.012+0.036=0.048⟹\text{Clearance fit}\end{array}$$

3. We have

$$\begin{array}{rl}\varphi 35\text{ H}7& \equiv \varphi 35_{0.000}^{+0.025}\\ \varphi 35\text{ r}6& \equiv \varphi 35_{0.0004}^{+0.050}\\ \text{Minimum clearance}& =0.035-0.025=0.01⟹\text{Interference fit}\end{array}$$