Primitive Motor with a Load

Stationary Case

Let’s consider a situation where we have a stationary motor supporting a load:

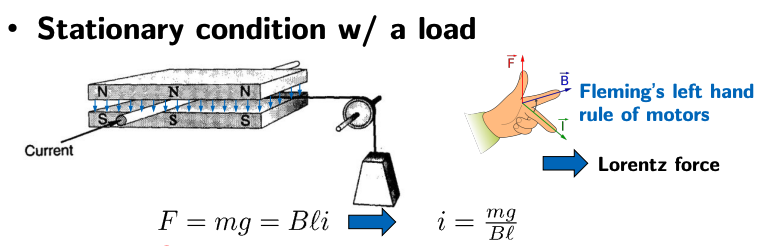
The load exerts a force $F$ (due to gravity), which is balanced by the electromagnetic force generated by the motor, which is determined by the current $i$ through the conductor:

$$F=mg=Bli$$

where $B$ is magnetic flux density, $l$ is the length of the conductor, and $i$ is the current.

The current required to support the load can then be found with

$$i=\frac{mg}{Bl}$$

Let’s consider the power. If the resistance of the conductor is $R$, the voltage across it is $V_1=iR$. The total electrical power supplied is $i^{2}R$, but since the motor is stationary, there is no mechanical work being done, so

$$\text{Mechanical power = 0}$$

which means that all the electrical energy is converted to heat due to the resistance of the conductor.

Constant Speed Case

What if the conductor is moving at a constant speed $v$ while carrying the same current $i$?

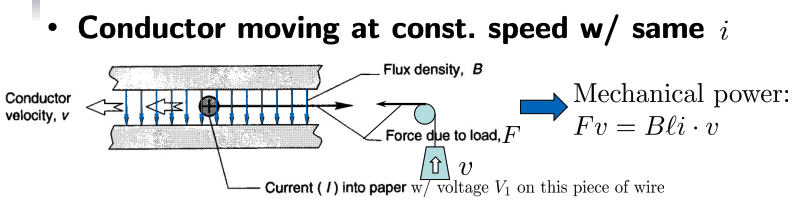
The mechanical power can be derived from force and velocity here:

$$Fv=Bli\cdot v$$

The total power is split into two components:

1. Electrical power input to overcome resistance $V_{1}i$
2. Electrical power input to produce mechanical work $Bliv$

Therefore, we have:

$$V_{2}i=V_{1}i+Bliv$$

where $V_2$ is the total supply voltage provided to the motor and $V_1$ is the resistive voltage drop across the conductor.

This also gives us

$$V_2-V_1=Blv=E\text{ (emf)}$$

So we see that the voltage difference is the equal to the electromotive force induced by the moving inductor.

Unlike the stationary case where force is dictated by current, in the moving case, the motor’s velocity is dictated by the voltage across it. The efficiency of the motor is given by the ratio of mechanical power to total electrical power supplied:

$$\eta =\frac{(V_2-V_1)i}{V_{2}i}=\frac{Blv}{V_2}=\frac{E}{V_2}$$