Gear Nomenclature

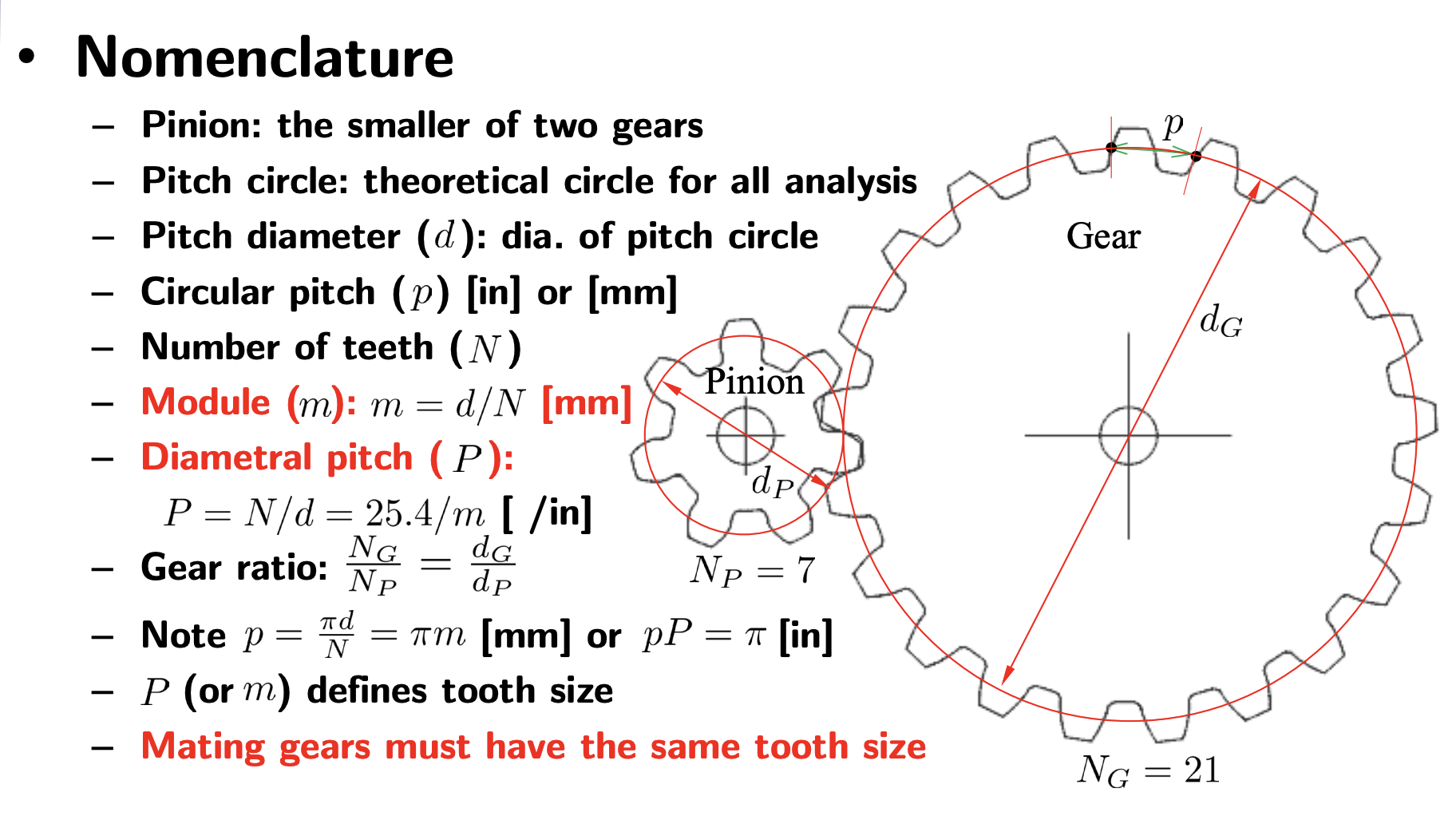
Nomenclature

• Pinion: The smaller of two gears. The larger is often called the gear.
• Pitch circle: Theoretical circle for analysis. The pitch circles of a pair of mating gears are tangent to each other.
• Pitch diameter ($d$): Diameter of pitch circle
• Circular pitch ($p$): Distance between teeth. Measured from the from a point on one tooth to a corresponding point on an adjacent tooth. This can be thought of as the sum of the tooth thickness and the width of space.
  • Units of $[\text{in}]$ or $[\text{mm}]$
  • Note that $p=\pi d/N=\pi m$ (circumference divided by number of teeth)
• Number of teeth ($N$)
• Module ($m$): $m=d/N[\text{mm}]$.
• Diametrical pitch ($P$): Number of teeth divided by diameter. $P=N/d=25.4/m[/\text{in}]$
  • This includes a conversion from mm to in, since 1 in = 25.4 mm
  • Note that $pP=\pi [\text{in}]$
• Gear ratio: $\frac{N_G}{N_P}=\frac{d_G}{d_P}$
• Addendum ($a$): Radial distance between the top land and the pitch circle.
• Dedendum ($b$): Radial distance from the bottom land to the pitch circle.
• Whole depth ($h_t$): Sum of the addendum and dedendum
• Clearance circle: Circle that is tangent to the addendum circle of the mating gear.
• Clearance ($c$): Amount by which the dedendum in a given gear exceeds the addendum of its mating gear.
• Backlash: Amount by which the width of a tooth space exceeds the thickness of the engaging tooth measured on the pitch circles.
• Mating gears must have the same tooth size

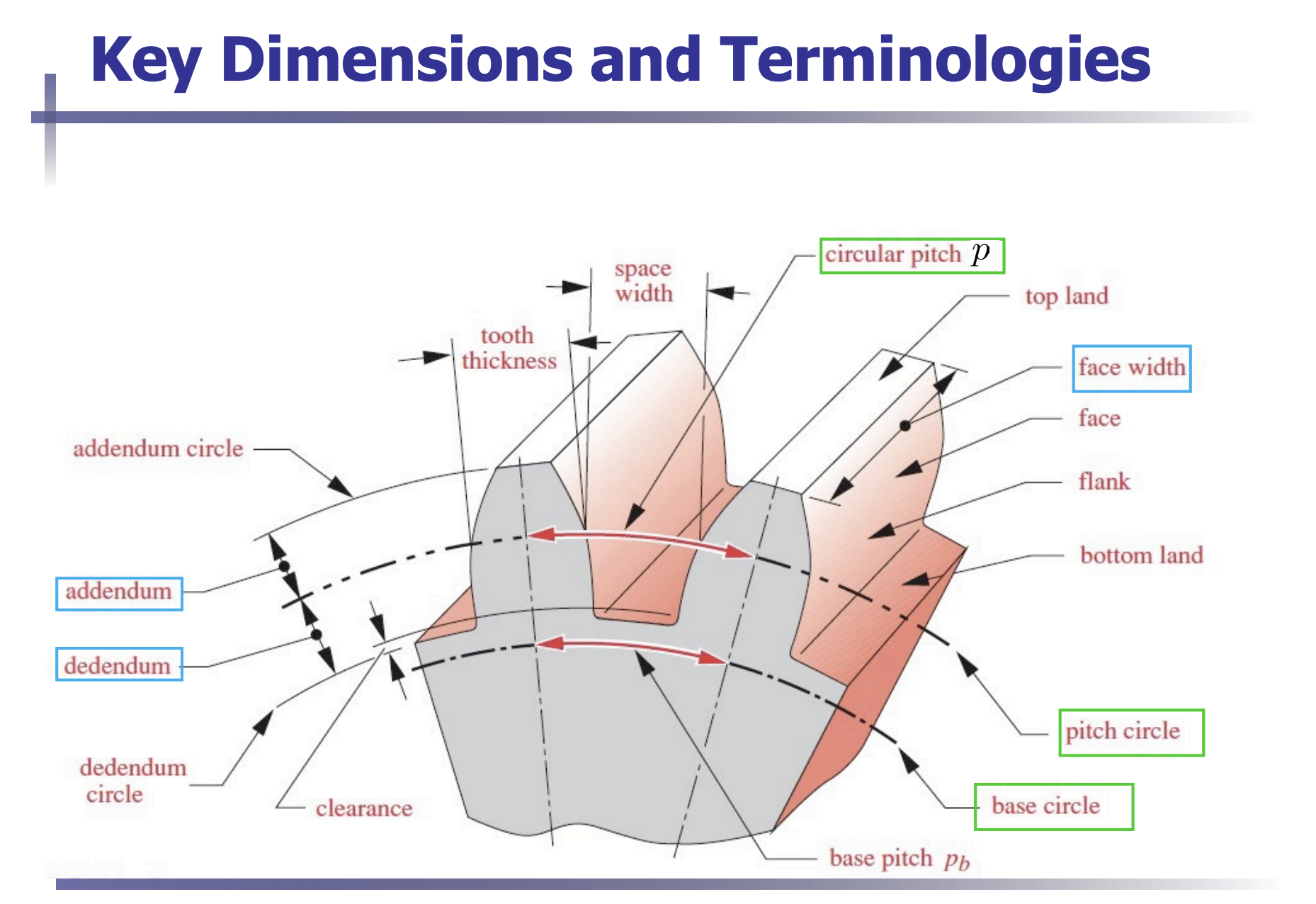
• Addendum $a=\frac{1}{P}$, Dedendum $b=\frac{1.25}{P}$
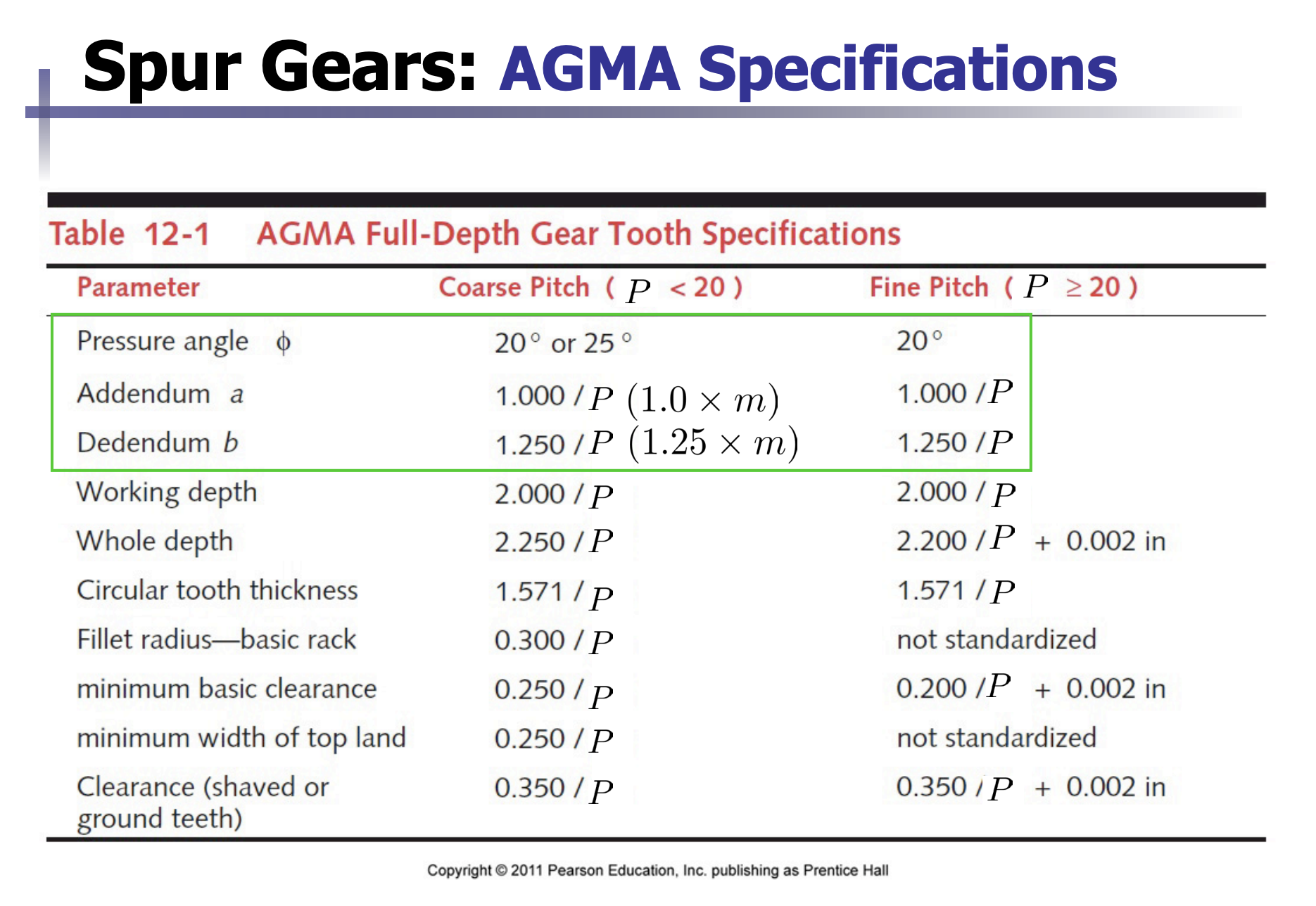
• Pressure angle typically $20°$

Example: Basic Gear Parameters

Question

A gearset consists of a 16-tooth pinion driving 40-tooth gear. The diametral pitch is 2 and pressure angle $20°$.

• (a) Compute circular pitch, center distance, radii of base circles
• (b) Compute addendum and dedendum
• (c) In mounting this gear set, the center distance was incorrectly made 1/4 inch larger. Compute the new values of the pressure angle and the pitch-circle diameters.

We have:

$$N_P=16,N_G=40,P=2,\varphi =20°$$

Since $P=25.4/m$, we have $m=25.4/P=12.7$.

(a) We can calculate circular pitch to be:

$$p=\frac{\pi d}{N}=\frac{\pi }{P}=\frac{\pi }{2}=1.571\text{ in}$$

Center distance is:

$$c=\frac{d_P}{2}+\frac{d_G}{2}=\frac{N_P/p}{2}+\frac{N_G/p}{2}=\frac{16/2}{2}+\frac{40/2}{2}=14\text{ in}$$

Base circle radii:

$$\begin{array}{rl}(r_b{)}_G& =\frac{d_G}{2}\cos \varphi =\frac{20}{2}\cos 20°=9.397\text{ in}\\ (r_b{)}_P& =\frac{d_P}{2}\cos \varphi =\frac{8}{2}\cos 20°=3.759\text{ in}\end{array}$$

(b) Addendum:

$$a=\frac{1}{P}=\frac{1}{2}=0.5\text{ in}$$

Dedendum:

$$b=\frac{1.25}{P}=0.625\text{ in}$$

(c) The center distance was made a 1/4 inch larger, so we have:

$$c=\frac{d_P^{\prime }+d_G^{\prime }}{2}=14.25\text{ in}$$

We still have the same gear ratio:

$$\frac{d_G^{\prime }}{d_P^{\prime }}=\frac{40}{16}$$

Solving this gives:

$$d_P^{\prime }=8.143\text{ in},d_G=20.357\text{ in}$$

Since the base circle remains the same, we have

$$\begin{array}{rl}{r}_b& =r^{\prime }\cos {\varphi }^{\prime }\\ {\varphi }^{\prime }& ={\cos }^{-1}\frac{(r_b{)}_p}{d_P^{\prime }/2}\\ & ={\cos }^{-1}\frac{3.759}{8.143/2}\\ & =22.59°\end{array}$$