<%tp.file.title%>

Drag Forces on Smooth Spheres and Cylinders

The plot below shoes the drag coefficient $C_D$ on the $y$-axis versus the Reynolds number $\text{Re}$ on the $x$-axis for smooth spheres (solid line) and smooth cylinders (dashed line).

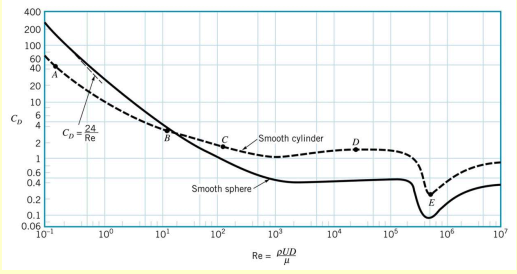
Point A: Laminar/Creeping Flow

At this point, we have $\text{Re}<1$.

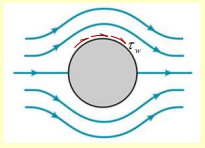
• Fluid moves smoothly around the sphere
• No separation or vortex formation
• Flow is viscous dominated, with inertial forces being negligible

The drag force is governed by Stokes Law:

$$F_D=6\pi \mu RV$$

Point B: Separation and Vortex Formation

Here, we have $10<\text{Re}<100$.

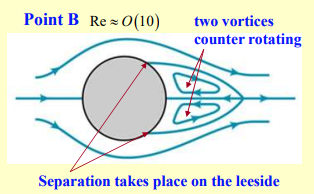
• Flow starts to separate at the rear of the sphere. Two counter-rotating vortices form, creating a low-pressure region.
• This introduces pressure drag in addition to shear drag; drag force is mainly due to the pressure difference
• Pressure inside the bubbles is very low

Point C: Oscillating Vortex Wake

In this region we have $100<\text{Re}<1000$:

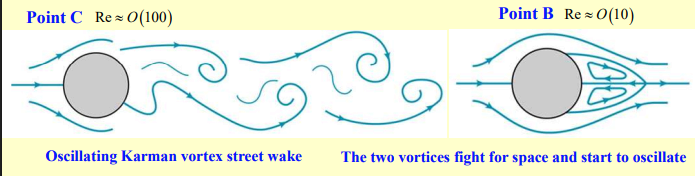
• A Kármán Vortex Street forms, characterized by alternating vortices shed behind the object. These vortices create an oscillating wake, introducing unsteady forces.

Point D: Turbulent Wake and Drag Crisis

Reynolds number: Approximately $10^3<\text{Re}<10^5$

• The separation point shifts backward and reach their limit position, reducing the size of the low-pressure wake.
• The flow inside the wake is turbulent
• Drag force is pressure dominated
• Flow physics remains the same $C_D=\text{const}$

Point E: Fully Turbulent Boundary

Reynolds number: $\text{Re}>10^5$.

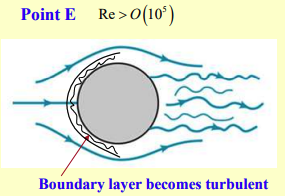
• The boundary layer is now completely turbulent.
• Separation points are pushed even further back, creating a narrower wake.
• Momentum transfer to the fluid is more effective.