Internal Stability for Feedback Systems

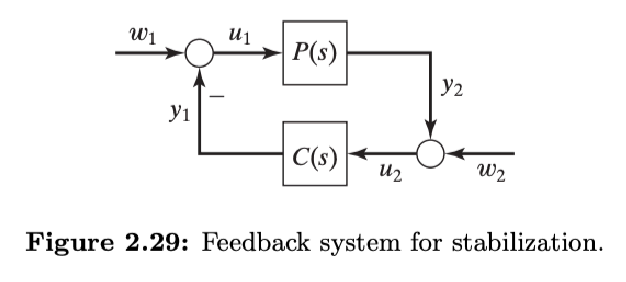
The system is said to be internally stable if the 8 transfer functions from $w_i,i=1,2$ to $y_j,j=1,2$ are stable. However, since they are written in terms of the Gang of Four, we only need to check the stability of these transfer functions when testing the closed-loop stability.

Let us have

$$P(s)=\frac{b(s)}{a(s)},C(s)=\frac{q(s)}{p(s)}$$

where $a(s)$ and $b(s)$ are coprime polynomials and so are $p(s)$ and $q(s)$.

Then we can write the gang of four matrix as

$$\text{GoF}(s)=\left[\begin{array}{cc}\frac{1}{1+P(s)C(s)}& \frac{C(s)}{1+P(s)C(s)}\\ \frac{P(s)}{1+P(s)C(s)}& \frac{P(S)C(s)}{1+P(s)C(s)}\end{array}\right]=\frac{\left[\begin{array}{cc}a(s)p(s)& a(s)q(s)\\ b(s)p(s)& b(s)q(s)\end{array}\right]}{a(s)p(s)+b(s)q(s)}$$

Let $P(s)$ and $C(s)$ these be proper transfer functions and assume that $1+P(\infty )Q(\infty )\ne 0$. Then, the following statements are equivalent:

1. The closed-loop system is internally stable.
2. The polynomial $a(s)p(s)+b(s)q(s)$ is stable.
3. There is no unstable pole/zero cancellation forming the product $P(s)C(s)$ and any of the gang of four is stable.

Character Polynomial

For a feedback system for stabilization with $P(s)=\frac{b(s)}{a(s)}$ and $C(s)=\frac{q(s)}{p(s)}$, the polynomial $c(s)=a(s)p(s)+b(s)q(s)$ is called its characteristic polynomial.

This is also equivalent to $1+P(s)C(s)=c(s)$ since

$$\begin{array}{rl}c(s)& =1+\frac{b(s)}{a(s)}\cdot \frac{q(s)}{p(s)}\\ & =\frac{a(s)p(s)+b(s)q(s)}{a(s)p(s)}\\ & =a(s)p(s)+b(s)q(s)\end{array}$$

Example