Electrical Systems Overview

Current

Current if the flow of electrons. It is given by:

$$\begin{array}{rl}i& =\frac{dQ}{dt}\\ Q(t)& =\int idt\end{array}$$

where $Q$ is the charge (number of electrons). Current is given in units of amperes A.

Voltage

Energy is required to move a charge between two points in a circuit. The work per unit charge required to do this is called voltage. The unit of voltage is the volt (V), which is defined to be one joule per coulomb. The voltage difference between two points in a circuit is a measure of the energy required to move charge from one point to the other

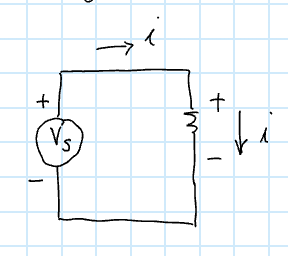
Direction of Current

Positive current is defined to go:

• From $+$ to $-$ in a circuit
• From $-$ to $+$ in a battery

Power

Power generated, dissipated, or stored by a circuit element equals the product of the voltage difference across the element and the current flowing through the element:

$$P=iv$$

Governing Laws

1. Kirchoff’s Current Law (Conservation of Charge): The algebraic sum of currents at any node is zero.
2. Kirchoff’s Voltage Law (Conservation of Energy): The algebraic sum of voltage across elements in a loop is zero.

Passive Elements

Resistors

When a current flows through wire or other circuit elements, it encounters resistance. Sometimes this resistance is desirable and intentionally introduced; a resistor is an element designed to provide resistance, such that there is a linear relation between the current passing through them and the voltage difference across them:

$$v=iR$$

The power dissipated by a resistor is given by

$$P=iv=i^{2}R=\frac{v^2}{R}$$

Parallel resistors:

$$\frac{1}{R_{\text{eq}}}=\frac{1}{R_1}+\frac{1}{R_2}$$

For parallel resistors, we should note that:

$$\frac{i_1}{i_2}=\frac{R_2}{R_1}$$

where $i_1$ and $i_2$ are the currents flowing through $R_2$ and $R_1$ respectively.

Series resistors:

$$R_{\text{eq}}=R_1+R_2$$

Capacitors

A capacitor is designed to store charge. The capacitance $C$ of a capacitor is a measure of how much charge can be stored for a given voltage difference across the element:

$$C=\frac{Q}{v}$$

Thus, we also have:

$$Q=\frac{1}{C}v=\frac{1}{C}\int idt$$

which gives:

$$i=C\frac{dv}{dt}$$

Capacitors store electrical energy as stored charge:

$$\begin{array}{rl}E& =\int Pdt\\ & =\int ivdt\\ & =\int vC\frac{dv}{dt}dt\\ & =C\int vdv\\ & =\frac{C}{2}{v}^2=\frac{1}{2}C{v}^2\end{array}$$

Inductor

A magnetic field (a flux) surrounds a moving charge or current. If the conductor of the current is coiled, the flux created by the current in one loop affects the adjacent loops. This flux is proportional to the time integral of the applied voltage, and the current is proportional to the flux.

The relation for an inductor is $\varphi =Li$, where $L$ is the inductance and $\varphi$ is the flux across the inductor. We can re-arrange this as:

$$L=\frac{\varphi }{i}\text{or}i=\frac{\varphi }{L}=\frac{1}{L}\varphi$$

The relation between flux and voltage is

$$\varphi =\int vdt$$

Combining the two relations above gives:

$$i=\frac{1}{L}\int vdt$$

which is equivalent to

$$v=L\frac{di}{dt}$$

Inductors store electrical energy in a magnetic field, which can be expressed as:

$$\begin{array}{rl}E& =\int Pdt\\ & =\int vidt\\ & =L\frac{i^2}{2}=\frac{1}{2}L{i}^2\end{array}$$

Examples