DAC Errors

We defined parameters for DAC specification; what are some errors DACs suffer from?

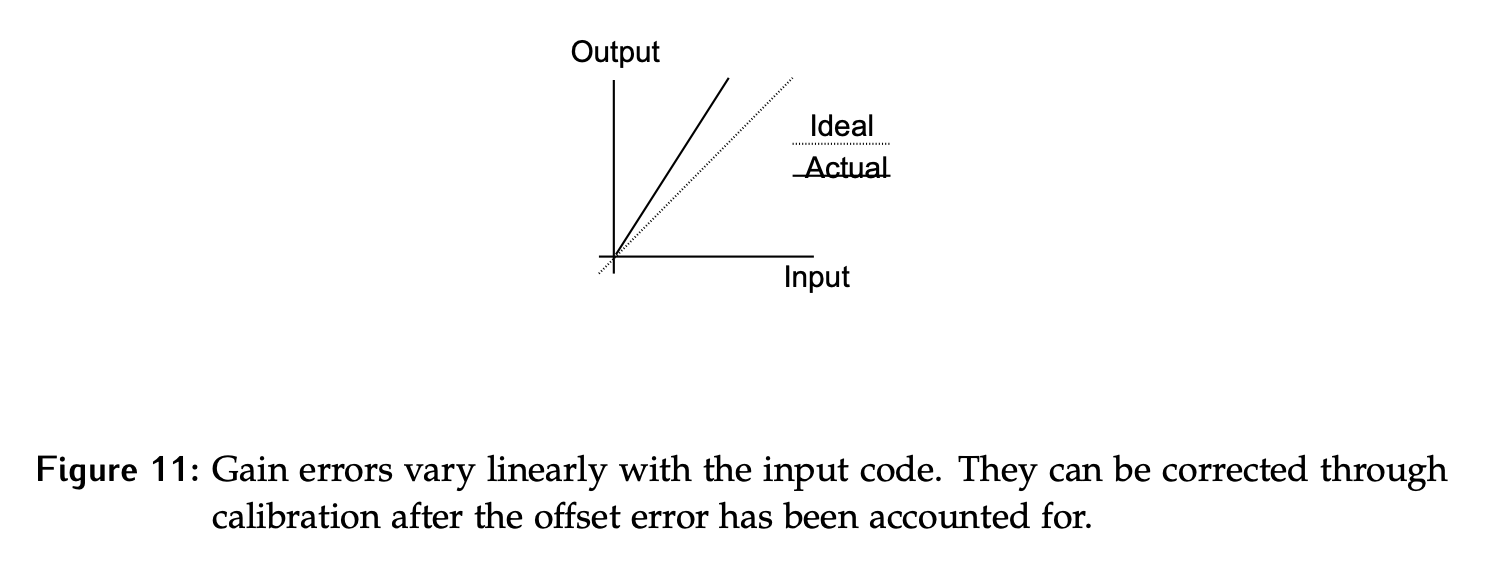
Gain and Offset Errors

Gain and offset errors are not dependent on the input code.

Offset Error

The offset error is defined as an analog shift in the output of the DAC that is constant over the full range of the digital input values. It can be caused by non-ideal properties of circuits such as leakage currents in switches, bias currents at the internal op-amp, and temperature sensitivities. It may be specified in many ways, including as a voltage, as a percentage or as a fraction of an LSB.

Since this is a fixed offset, a calibration can be done to correct it. A measurement of the output of the DAC when the input code is 0 will tell you what the offset is as shown in Figure 10. Subtracting this amount from all outputs will negate the error.

Gain Error

The gain error is defined as an error that varies linearly with the input code. This error is often sensitive to temperature and will not be consistent between uses of the device. It must be calibrated for each time, preferably after the device has warmed up.

Gain error can also be corrected through calibration. We need to correct for the offset error first, so that the ideal output is achieved at the 0 input code. Then, we can take a measurement at the maximum code, and then calculate the scaling factor required to correct it to the ideal value. The error can then be removed from the DAC outputs by multiplying them by this gain error.

Many DACs have calibration registers that allow offset and gain factors to be set so that they can be applied to the output of the signal at the output of the DAC before the final analog signal is passed out of the chip.

Mathematical Description

Mathematically, the ideal relationship would be:

$$V_{\text{out}}=V_{\text{ideal}}=k{V}_{\text{ref}}B$$

Offset error means we have:

$$V_{\text{out}}^{\text{offset error}}=V_{\text{ideal}}+V_{\text{offset}}$$

We can calibrate this by subtracting the offset at 0 output:

$$V_{\text{out}}^{\text{offset calibrated}}=V_{\text{ideal}}+V_{\text{offset}}-V_{\text{zero-code}}$$

Then, the gain error is:

$$V_{\text{out}}^{\text{gain error}}=V_{\text{out}}^{\text{offset calibrated}}\times \text{Gain Error}$$

To fix this, we multiply by the ratio of the actual maximum output voltage to the ideal maximum output voltage:

$$V_{\text{out}}^{\text{gain calibrated}}=V_{\text{out}}^{\text{offset calibrated}}\times \text{Gain Error}\times \frac{\text{FSAR}}{V_{\text{max}}^{\text{actual}}}$$

Linearity Errors

After correcting for gain and offset errors, the 0 and max codes align with their ideal values. However, the values in between are not correctable. Linearity errors affect each code differently, and thus cannot be calibrated.

DNL

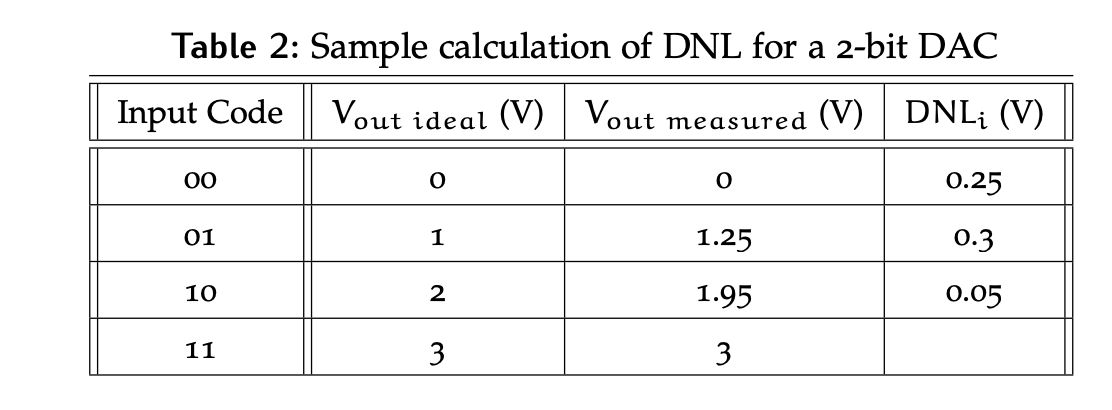
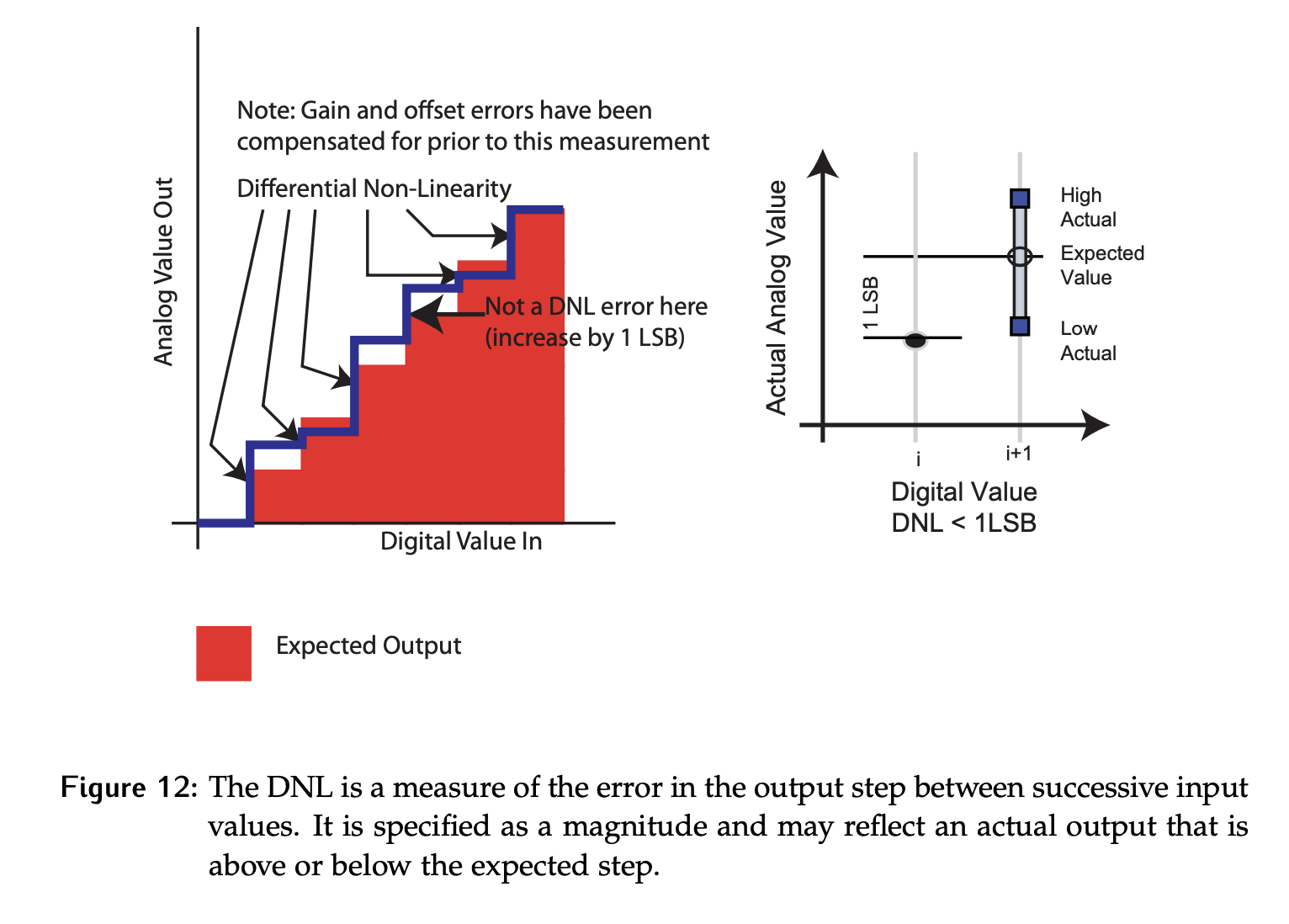
Differential Non-Linearity (DNL) is a measure of the error in the steps between codes, which ideally should all be 1 LSB. This error is specified as an absolute value, so it tells us the possible deviation above or below an ideal step. It is commonly specified on the data sheet for DAC devices, and may have both a typical and maximum value.

To calculate the DNL, the deviation in ideal step value as the input value is increased to the successive one must be calculated. This means there will be $2^n-1$ calculations required. The error in each step is found by measuring the outputs for all input values, $V_i$, then taking:

$$\begin{array}{rl}\text{Real difference between steps:}& \Delta V_i=V_{\text{out}}(i+1)-V_{\text{out}}(i)\\ \text{Ideal difference between steps:}& \Delta V_{\text{ideal}}\\ \text{DNL:}& \Delta V_i-\Delta V_{\text{ideal}}\end{array}$$

For the device overall, the DNL is then specified to be the largest of the individual values as it is the worst case that is most meaningful in characterizing the quality. So, in general we have:

$$\text{DNL}=\max (|(V_{\text{out}}(i+1)-V_{\text{out}}(i))-\Delta V_{\text{ideal}}|)$$

Note that the gain and offset errors must be accounted for first, or the DNL calculated will include these errors, as they compound on each other.

Imagine a 2-bit DAC with the outputs shown in Table 2 after gain and offset calibration. After calculating the DNL for each step, the DNL for the device will be specified as 0.3 V as it is the maximum value.

What does DNL mean? If we have DNL = 1 LSB, moving from $B=i$ to $B=i+1$ will result in a change of output between $1\pm 1$ LSBs in magnitude, or 0 to 2 LSBs.

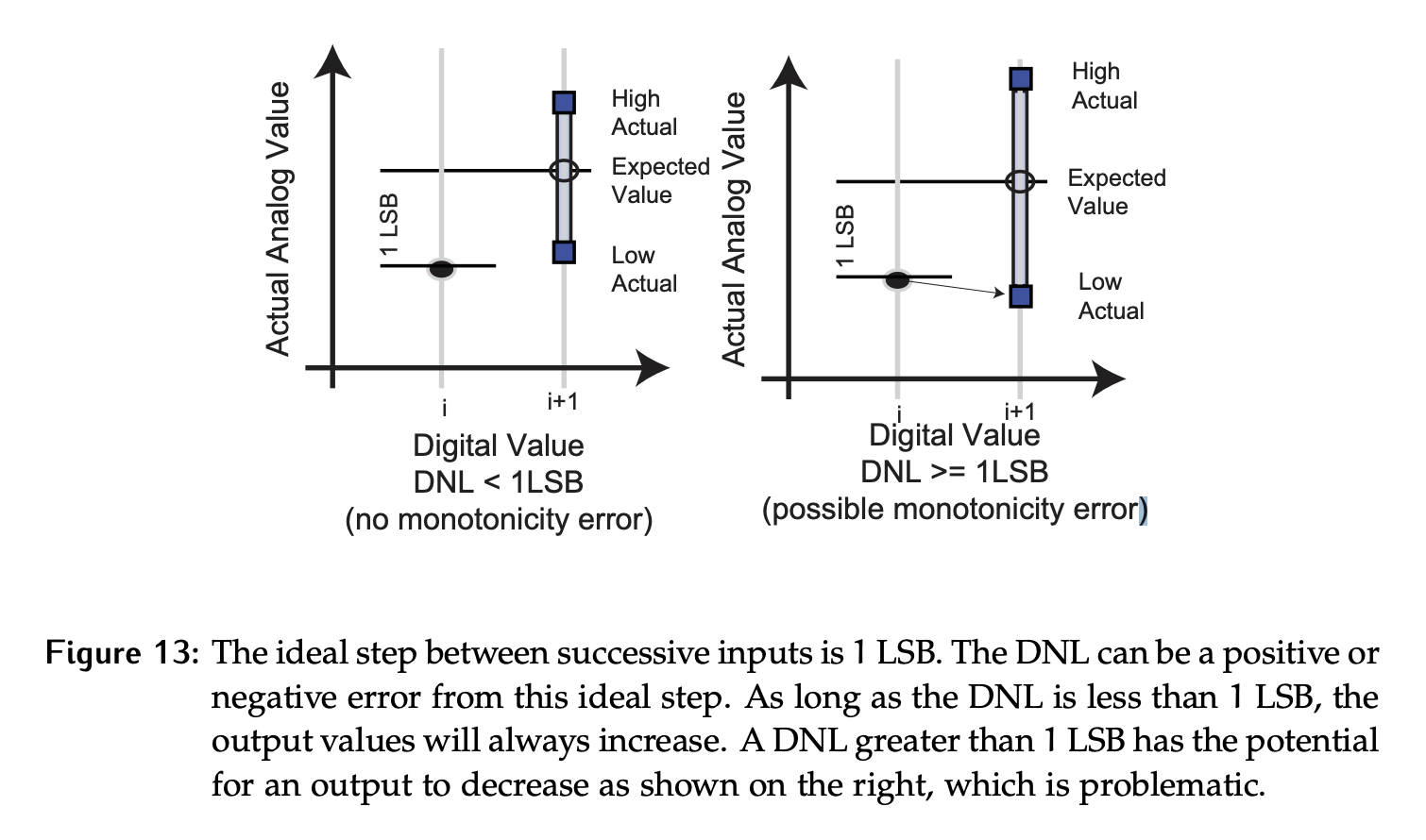
The expected output of the DAC is that as the input codes increase, the output voltage should also increase. However, if the DNL is large enough (more than 1 LSB), an increase in input code can result in a decrease in output value. This is known as monotonicity error and indicates a DAC of very poor quality. Some DNL datasheets will say “guaranteed monotonic”, which means DNL is less than 1 LSB.

ILE

Integral linearity error (ILE) also affects each code differently. This is a measure of the error within the code itself – how far does the output deviate from the ideal output for a given input code?

Once again, the ILE is defined as the absolute value taken from the worst case:

$$\text{ILE}=\max (|V_{\text{out measured}}(i)-V_{\text{out ideal}}(i)|)$$

Dynamic Errors

We also need the dynamic performance of the devices – how do they behave as the input codes are changing?

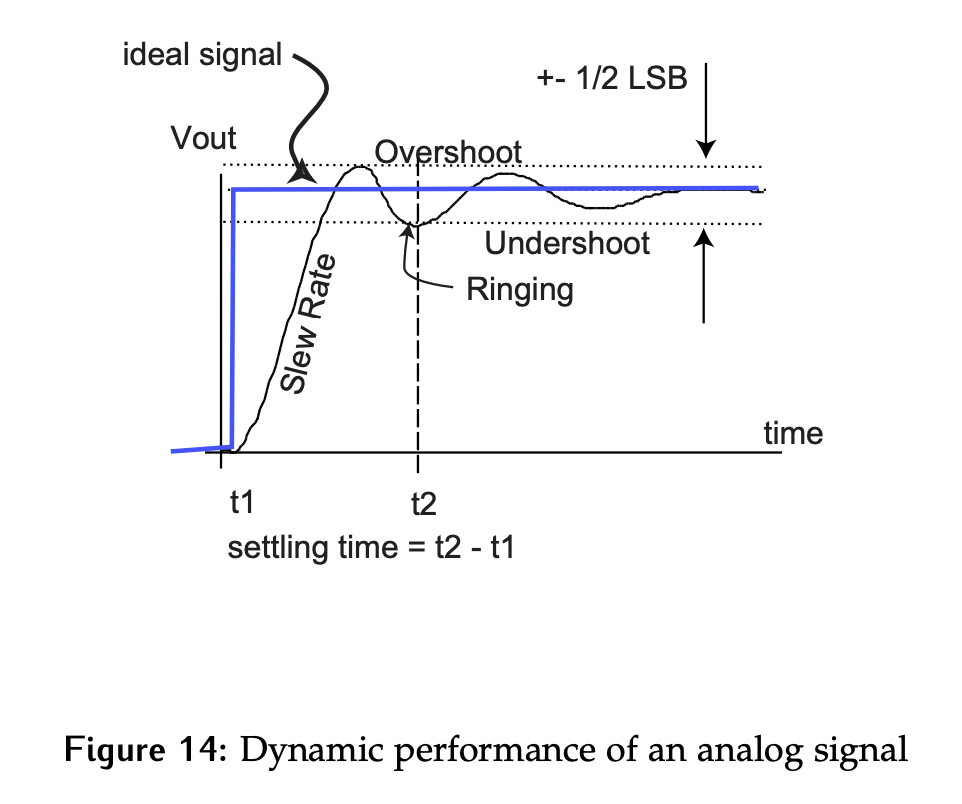
Recall that the settling time characterized the time for a signal to change from the minimum to maximum output value. For electronics, the definition of “settled” is modified from the 10% of max to be $\pm 0.5\text{ LSB}$.

In the case of DACs, the settling time is mostly dictated by the performance of the output amplifier used to drive the final analog signal. As a result, DACs often leave off the final output amplifier, and require the user to add an external device. This makes the devices cheaper, appear faster, and more versatile.

Glitch

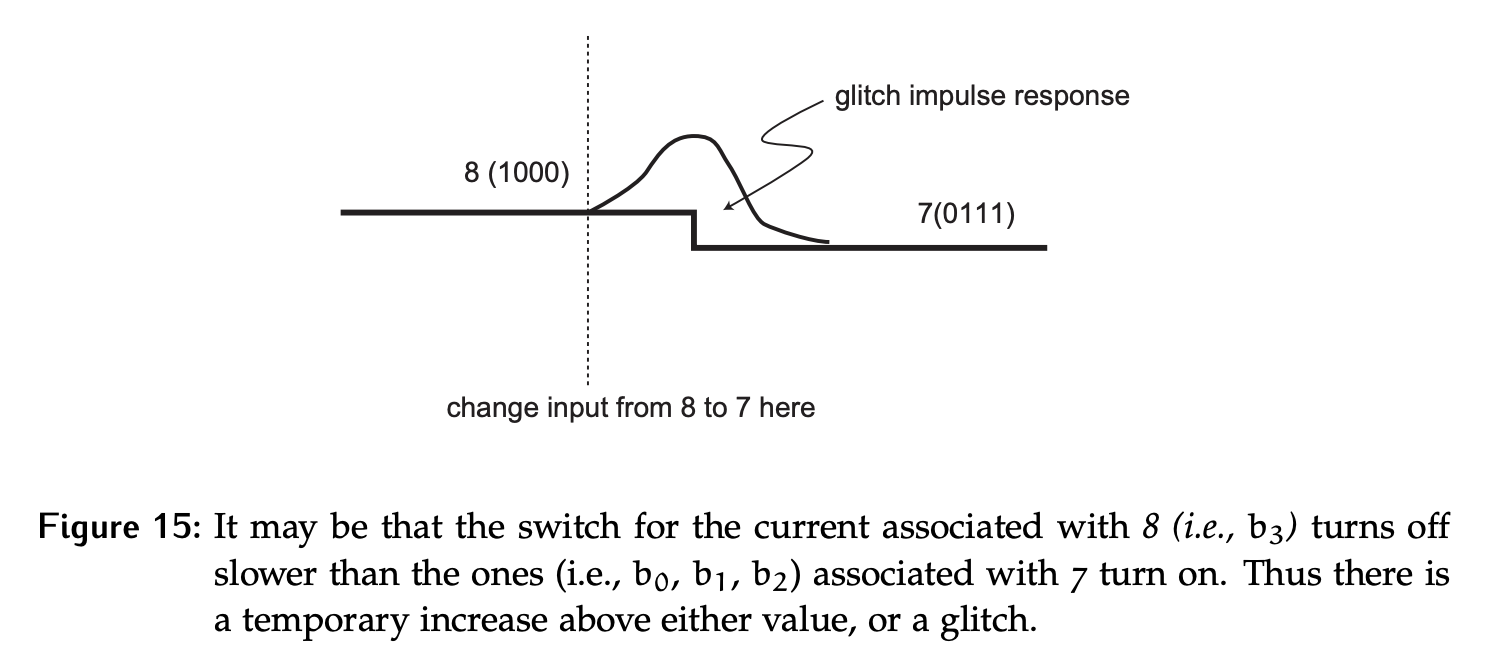
A glitch is an unintended change in the output value due to variations in the times when the inputs changed and/or variations in delay through the signal path.

In the case of the DAC, the bits in the binary input code may not all change simultaneously. When many bits are changing, this can result in unintended input values being present for brief periods of time. Take the case of moving from an input code of 8 to 7 in a 4-bit DAC, where all 4 bits need to change (1000 → 0111). If the MSB flips first, a code of 1111 is briefly seen by the DAC, which could cause the analog output level to start rising. The code won’t be present long enough to reach the maximum analog output, but this unintended increase could exceed a threshold prematurely and effect downstream logic (especially for an ADC).

The conversion time is the total time from when the inputs are set to when the analog output is stable. For the DAC designs considered here, this will be the settling time of the op-amp, as well as the time it took the switches controlled by the binary value to respond.

• Why does conversion time time matter? If we try to change our inputs at a rate that exceeds this time, the output will be garbage. The device will constantly be trying to adjust to the change, but never settling before the next change comes.