Plane Stress Transformation

Taking our 3D stress element, and cutting it with an oblique plane with a normal $n$ at some arbitrary angle $\varphi$ counter-clockwise from the $x$-axis produces a 2D stress element:

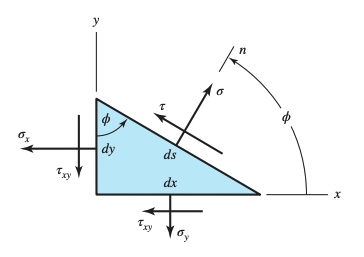
By summing the forces caused by all the stress components to zero, the stresses $\sigma$ and $\tau$ are found to be:

$$\begin{array}{rl}\sigma & =\frac{{\sigma }_x+{\sigma }_y}{2}+\frac{{\sigma }_x-{\sigma }_y}{2}\cos 2\varphi +{\tau }_{xy}\sin 2\varphi \\ \tau & =-\frac{{\sigma }_x-{\sigma }_y}{2}\sin 2\varphi +{\tau }_{xy}\cos (2\varphi )\end{array}$$

These are called the plane-stress transformation equations.

Principal Stresses and Directions

We can maximize $\sigma$ by differentiate the expression for $\sigma$ above and setting this equal to zero. This gives:

$$\tan 2{\varphi }_p=\frac{2{\tau }_{xy}}{{\sigma }_x-{\sigma }_y}$$

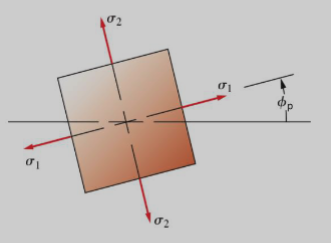
This gives the two principal directions associated with two principal stresses; one is the maximum normal stress, and one is the minimum. The angle between the principal directions is $90°$.

These principal stresses can be found with:

$${\sigma }_1,{\sigma }_2=\frac{{\sigma }_x+{\sigma }_y}{2}\pm \sqrt{{\left(\frac{{\sigma }_x-{\sigma }_y}{2}\right)}^2+{\tau }_{xy}^2}$$

At the principal stresses, the shear stress is zero! See Mohr’s Circle for geometric intuition.

Extreme-Value Shear Stresses

Similarly, the shear plane-stress transformation equation can be differentiated and set to zero to find:

$$\tan (2{\varphi }_s)=\frac{{\sigma }_x-{\sigma }_y}{2{\tau }_{xy}}$$

This is related to the principal planes by:

$${\varphi }_s=45°\pm {\varphi }_p$$

This gives us 2 extreme-value shear stresses:

$${\tau }_1,{\tau }_2=\pm \sqrt{{\left(\frac{{\sigma }_x-{\sigma }_y}{2}\right)}^2+{\tau }_{xy}^2}$$

At extreme-value shear stress configurations, the normal stress $\sigma$ takes on the value of ${\sigma }_{\text{avg}}=({\sigma }_x+{\sigma }_y)/2$.