Gruebler's Equation

Gruebler’s Equation states:

$$M=3L-2J-3G$$

where:

• $M$ is the degree of freedom or mobility
• $L$ is the number of links
• $J$ is the number of joints
• $G$ is the number of grounded links.

Iin any real mechanism, even if more than one link of the kinematic chain is grounded, the net effect will be to create one larger, higher-order ground link, as there can be only one ground plane. Thus, $G$ is always $1$, so Gruebler’s Equation becomes:

$$M=3(L-1)-2J$$

Gruebler’s equation holds for planar mechanisms, not 3D mechanisms.

Exceptions in Gruebler’s Equation

In rare instances, Gruebler’s Equation can yield misleading results as it does not consider the impact of link geometry.

In the example below, the DOF is zero using Gruebler’s Equation, implying that the mechanism is locked. However, with uniform-sized pivoted links and equal joint distances, this mechanism would have one degree of freedom, allowing for motion.

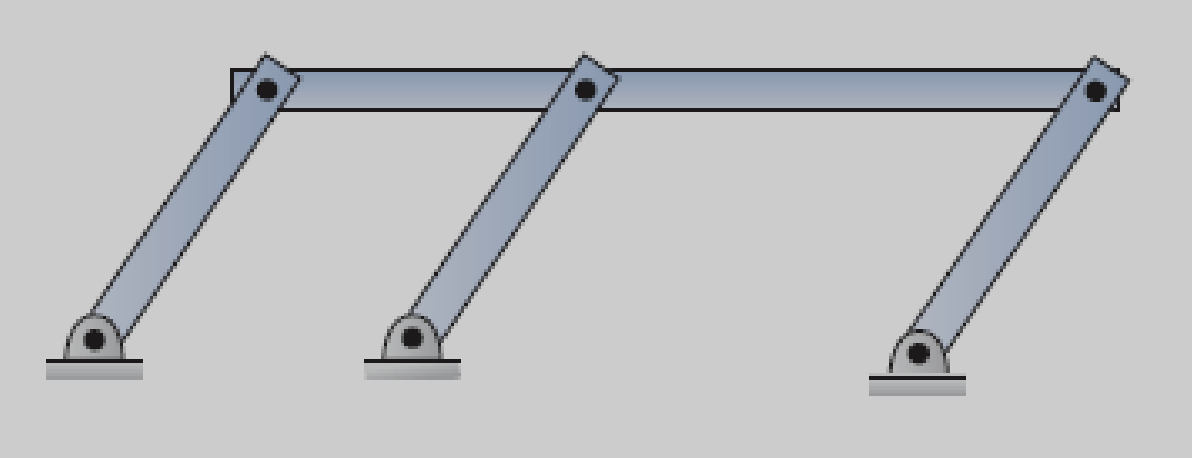
Kutzbach’s Modification

Kutzbach’s modification of Gruebler’s equation is:

$$M=3(L-1)-2J_1-J_2$$

where:

• $M$ is the degree of freedom or mobility
• $L$ is the number of links
• $J_1$ is the number of full joints (1 DoF)
• $J_2$ is the number of half joints (2 DoF)

Notes:

• Independent of link size or shape
• For multiple joints that are joined, we count as one less than the number of links joined and add this to $J_1$

Interpreting $M$ results

• $M>0$: We have a mechanism, with relative motion between links
• $M=0$: We have a structure, where no motion is possible
• $M<0$: We have a pre-loaded structure, where no motion is possible, and stress is present at time of assembly.