Force Analysis of Single Link

For a single link in pure rotation, the problem set-up first requires that we know:

• Angular and linear accelerations (determined through kinematic analysis)
• Mass of link
• Position information (link length, location of center of gravity)
• Mass moment of inertia with respect to center of gravity $I_G$

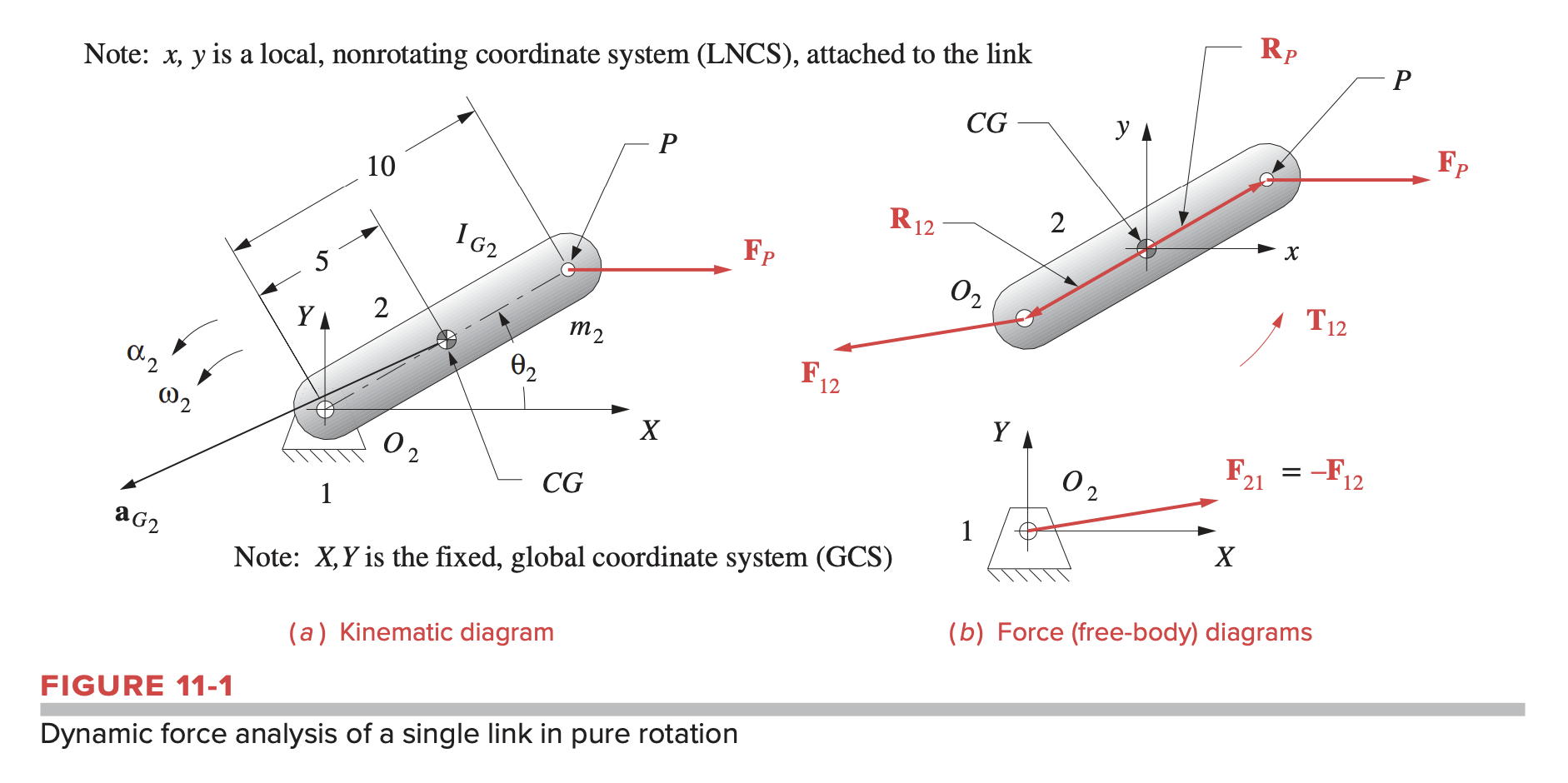
Then, we take the following steps:

• Set-up a non-rotating, local coordinate system (LNCS) at the member’s center of gravity
• Draw a FBD
• Establish position vectors to point of application of forces with respect to local coordinate system
• Determine position components according to local coordinate system. For example, in the FBD shown above in Fig 11-1 (b) we might write find the components of $R_{12}$ as $R_{12x}$ and $R_{12y}$.

Our unknowns are $F_{12x},F_{12y},T_{12}$. We can set up a set of equations based on N2L:

$$\begin{array}{rl}\text{Resultant force:}& \sum F=F_P+F_{12}=m_2{a}_G\\ \text{Resultant moment:}& \sum T=T_{12}+(R_{12}\times F_{12})+(R_P\times F_P)=I_G\alpha \mathbf{k}\end{array}$$

Note that the $\mathbf{k}$ is because the resultant moment acts in the $z$-dimension.

We can then write these in scalar forms:

$$\begin{array}{rl}{m}_2{a}_{Gx}& =F_{Px}+F_{12x}\\ m_2{a}_{Gy}& =F_{Py}+F_{12y}\\ I_{G\alpha }& =T_{12}+(R_{12x}{F}_{12y}-R_{12y}{F}_{12x})+(R_{Px}{F}_{Py}-R_{Py}{F}_{Px})\end{array}$$

This can be written in matrix form as a set of simultaneous linear equations:

$$\begin{array}{rl}\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ -R_{12y}& R_{12x}& 1\end{array}\right]& \times \left[\begin{array}{c}{F}_{12x}\\ F_{12y}\\ T_{12}\end{array}\right]=\left[\begin{array}{c}{m}_2{a}_{Gx}-F_{Px}\\ m_2{a}_{Gy}-F_{Py}\\ I_G\alpha -(R_{Px}{F}_{Py}-R_{Py}{F}_{Px})\end{array}\right]\\ \left[\begin{array}{c}\mathbf{A}\end{array}\right]& \times \left[\begin{array}{c}\mathbf{B}\end{array}\right]=\left[\begin{array}{c}\mathbf{C}\end{array}\right]\end{array}$$

We can then take the inverse of this matrix to solve for the unknowns in matrix B:

$$\left[\begin{array}{c}\mathbf{B}\end{array}\right]={\left[\begin{array}{c}\mathbf{A}\end{array}\right]}^{-1}\times \left[\begin{array}{c}\mathbf{C}\end{array}\right]$$