Force Analysis of Fourbar Linkage

For a fourbar linkage, the problem set-up first requires that we know:

Angular and linear accelerations (determined through kinematic analysis)
Masses of links
Position information (link lengths, link positions, location of center of gravity for each link)
Mass moment of inertia with respect to CG, $I_{G}$ , for each link

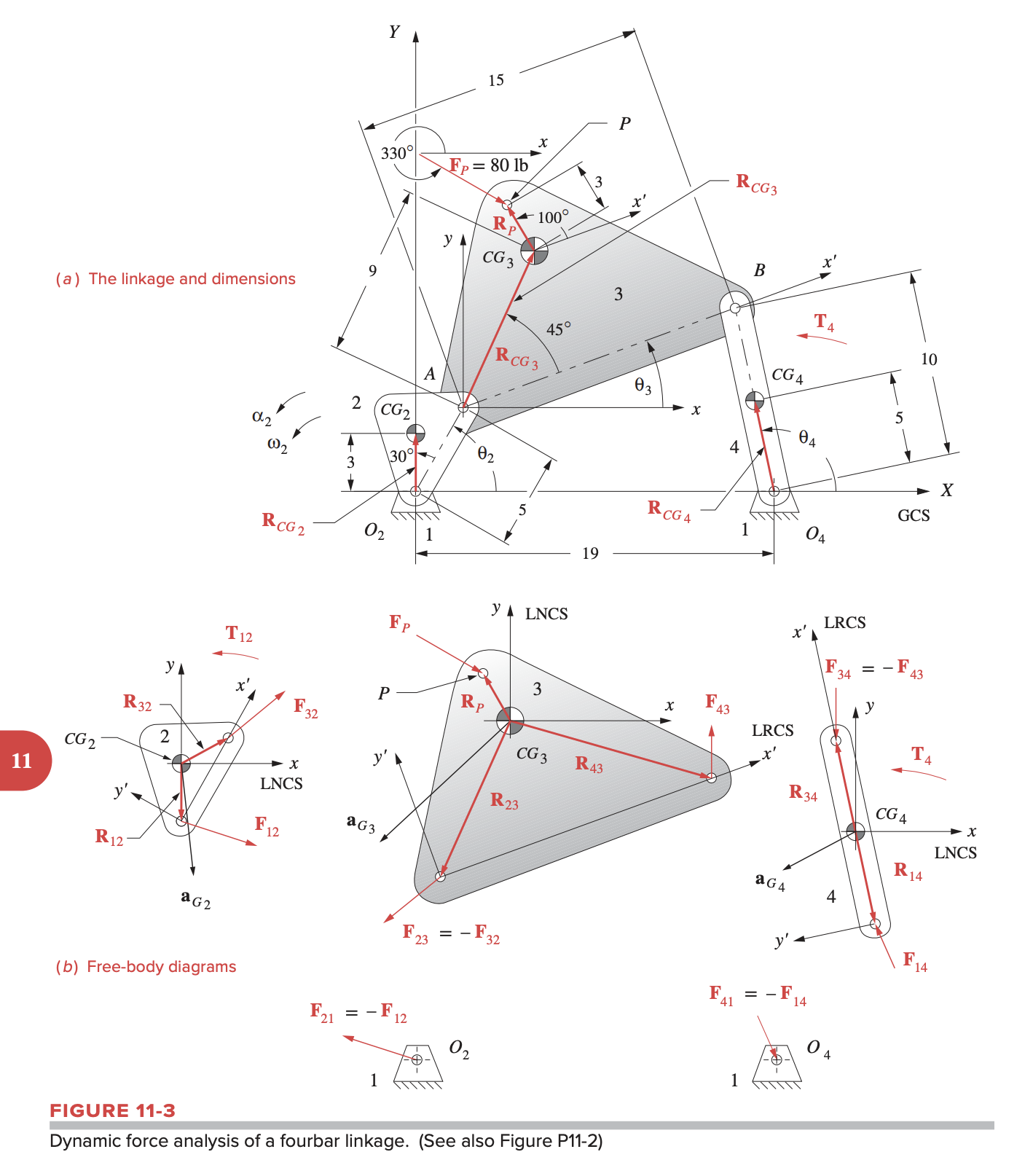
We then write out the forces and moments for each link.

Link 2:

F_{12 x} F_{12 y} T_{12} + F_{32 x} = m_{2} a_{G_{2 x}} + F_{32 y} = m_{2} a_{G_{2 y}} + (R_{12 x} F_{12 y} - R_{12 y} F_{12 x}) + (R_{32 x} F_{12 y} - R_{32 y} F_{32 x}) = I_{G_{2}} α_{2}

Link 3:

F_{43 x} F_{12 y} (R_{43 x} - F_{32 x} + F_{P x} = m_{3} a_{G_{3 x}} - F_{32 y} + F_{P y} = m_{3} a_{G_{3 y}} F_{43 y} - R_{43 y} F_{43 x}) + (R_{23 x} F_{32 y} - R_{23 y} F_{32 x}) + (R_{P x} F_{P y} - R_{P y} F_{P x}) = I_{G_{3}} α_{3}

Link 4:

F_{14 x} F_{14 y} (R_{14 x} - F_{43 x} = m_{4} a_{G_{4 x}} - F_{43 y} = m_{4} a_{G_{4 y}} F_{14 y} - R_{14 y} F_{14 x}) - (R_{34 x} F_{43 y} - R_{34 y} F_{43 x}) + T_{4} = I_{G_{4}} α_{4}

This can be written in matrix form as a simultaneous system of equation with 9 unknowns:

10 - R_{12 y} 000000 01 R_{12 x} 000000 10 - R_{32 y} - 1 0 R_{23 y} 000 01 R_{32 x} 0 - 1 - R_{23 x} 000 00010 - R_{43 y} - 1 0 R_{34 y} 00001 R_{43 x} 0 - 1 - R_{34 x} 00000010 - R_{14 y} 00000001 R_{14 x} 001000000 \times F_{12 x} F_{12 y} F_{32 x} F_{32 y} F_{43 x} F_{43 y} F_{14 y} F_{14 x} T_{12} = m_{2} a_{G_{2 x}} m_{2} a_{G_{2 y}} I_{G_{2}} α_{2} m_{3} a_{G_{3 x}} - F_{P x} m_{3} a_{G_{3 y}} - F_{p y} I_{G_{3}} α_{3} - R_{p x} F_{P y} + R_{P y} F_{P x} m_{4} a_{G_{4 x}} m_{4} a_{G_{4 y}} I_{G_{4}} α_{4} - T_{4}

[A] [B] = [C]

We can then take the inverse of the matrix to solve:

[B] = [A]^{- 1} [C]

/notes/