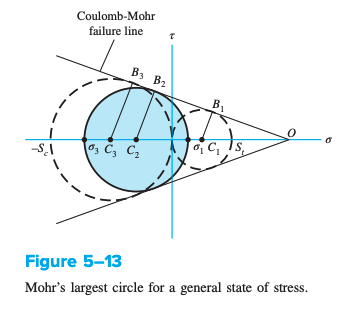
Coulomb-Mohr Theory

Coulomb-Mohr theory is for ductile materials where strength in tension does not equal strength in compression. Examples of this include magnesium alloys, gray cast irons.

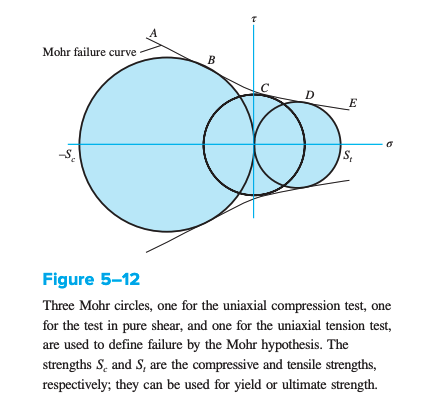
Mohr’s failure curve uses three tests for tension, compression and shear. The material undergoes these until it yields. Coulomb-Mohr is a variation, where the BCD boundary line is assumed to be straight, so that only tensile and compressive strengths are necessary.

General Case

In the general 3D case, we have three principal stresses ${\sigma }_1\ge {\sigma }_2\ge {\sigma }_3$. The yield conditions are:

$$\frac{{\sigma }_1}{S_t}-\frac{{\sigma }_3}{S_c}\ge 1$$

where $S_t,S_c$ are the ultimate tensile and compressive strengths of a material.

When designing with a factor of safety $n$:

$$\frac{{\sigma }_1}{S_t}-\frac{{\sigma }_3}{S_c}=\frac{1}{n}$$

Plane Stress

For plane stress, we have two principal stresses in the plane of analysis, such that ${\sigma }_A\ge {\sigma }_B$. The third principal stress is zero. We have 3 cases:

	Case 1: ${\sigma }_A\ge {\sigma }_B\ge 0$	Case 2: ${\sigma }_A\ge 0\ge {\sigma }_B$	Case 3: $0\ge {\sigma }_A\ge {\sigma }_B$
Stresses	${\sigma }_1={\sigma }_A$ and ${\sigma }_3=0$	${\sigma }_1={\sigma }_A$ and ${\sigma }_3={\sigma }_B$	${\sigma }_1=0$ and ${\sigma }_3={\sigma }_B$
Yield	${\sigma }_A\ge S_t$	$\frac{{\sigma }_A}{S_t}-\frac{{\sigma }_B}{S_c}\ge 1$	${\sigma }_B\le -S_c$
Design	${\sigma }_A=\frac{S_t}{n}$	$\frac{{\sigma }_A}{S_t}-\frac{{\sigma }_B}{S_c}=\frac{1}{n}$	${\sigma }_B=-\frac{S_y}{n}$

Shear Stress

For shear stress (pure shear, ${\sigma }_1=-{\sigma }_3=\tau$), we have yield conditions such that:

$$\begin{array}{rl}{\tau }_{max}& \ge S_{xy}\\ {\sigma }_1& =-{\sigma }_3\ge S_{xy}\end{array}$$

For design:

$$\begin{array}{r}{\tau }_{max}=\frac{S_{sy}}{n}\\ {\sigma }_1=-{\sigma }_3=\frac{S_{xy}}{n}\end{array}$$

Relationship between $S_{sy},S_{yt}$ and $S_{yc}$:

$$S_{sy}=\frac{S_{yt}{S}_{yc}}{S_{yt}+S_{yc}}$$