Rotational Motion

Angular Position, Velocity, and Acceleration

Position

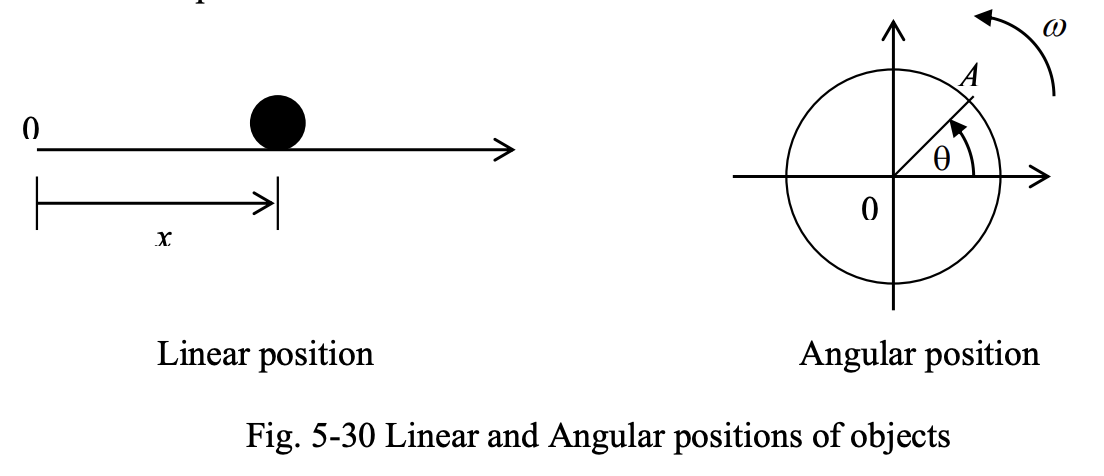
In linear motion, the distance or displacement of an object with respect to a reference point, in meters, is used to determine its position.

• A positive distance or displacement implies that the object is on the right-hand side of the reference point

In rotational motion, the position of a rotating object is determined by the angle, in degrees or radians, at which the object is oriented with respect to a reference axis.

• A positive angular displacement implies that the object is displaced with respect to the reference axis in the counterclockwise direction.

Velocity

In linear motion, speed, in meters per second, is defined as the rate of change of distance with respect to time:

$$v=\frac{dx}{dt}$$

In rotational motion, angular velocity, in radians per second, is defined as the rate of change of angular displacement with respect to time:

$$\omega =\frac{d\theta }{dt}$$

A positive angular velocity implies rotation in the counterclockwise direction.

A subscript is often added to clarify between physical/mechanical quantities and electrical ones, as some symbols like $\omega$ are used for both.

$$\begin{array}{rl}{\omega }_m& =\frac{d{\theta }_m}{dt}\text{Angular velocity (Rad/s)}\\ f_m& =\frac{{\omega }_m}{2\pi }\text{Angular velocity(Rev/s)}\\ n_m& =60f_m\text{Angular velocity(Rev/minute)}\\ {\omega }_m& =\frac{2\pi n_m}{60}\end{array}$$

Acceleration

In linear motion, acceleration, in meters per second squared, is defined as the rate of change of velocity with respect to time:

$$a=\frac{dv}{dt}$$

In rotational motion, angular acceleration, in radians per second squared, is defined as the rate of change of angular velocity:

$${\alpha }_m=\frac{d{\omega }_m}{dt}$$

Torque

In linear motion, force causes a change in the velocity of an object. A positive force accelerates the object, a negative force decelerates the object.

In rotational motion, torque (or twisting force) tends to change the angular velocity of an object that is free to rotate about its axis. A positive torque accelerates the object, whereas a negative torque decelerates the object. The figure below shoes the mechanism of development of torque when a force is exerted on an object which is free to rotate about its axis.

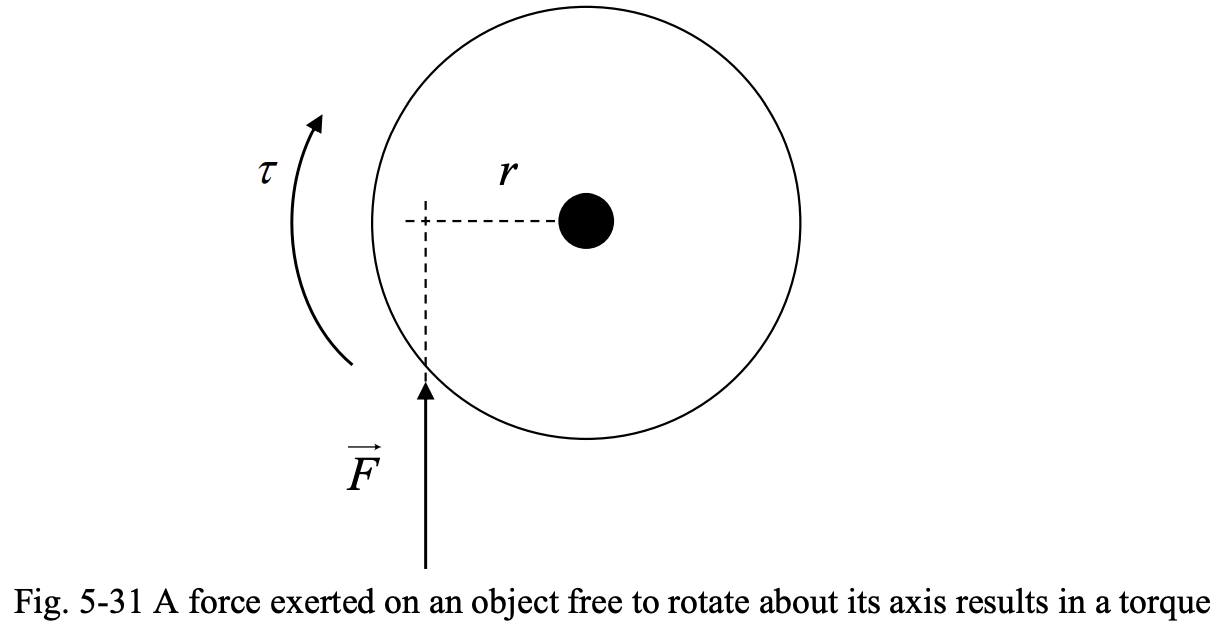
The force exerted on an object, the smaller (i.e. perpendicular) distance between the line of action and the axis of rotation of the object and the developed torque are related through:

$$\tau =F\times r$$

In SI units, force is measured in newtons ($N$), distance in meters ($m$), and torque in newton-meters ($N\cdot m$). The force $F$ acts at the distance $r$ from the axis of rotation and develops a clockwise torque on the object, which tends to accelerate the object in the clockwise direction.

Note that the magnitude of the developed torque depends on the magnitude of the force and the distance between the line of action of force and axis of rotation. The distance is a specification in the mechanical design of the electric machine and is fixed, whereas the force can be controlled during the operation of the machine by adjusting the current passing through the conductors and the magnetic field density.

Newton’s Law of Motion

In linear motion, the force exerted on an object, the mass of the object and the resulting object’s acceleration are related by Newton’s law of motion as:

$$F=ma$$

In SI units, force is in newtons ($\text{N}$), mass is in kilograms ($\text{kg}$) and acceleration is in meters per second squared ($\text{m}/{\text{s}}^2$).

In rotational motion, force changes to torque, linear acceleration changes to angular acceleration, and mass changes to moment of inertia, $J$. As mass resists changes in linear velocity, moment of inertia resists changes in angular velocity. Torque, moment of inertia and angular acceleration are related by Newton’s law of motion as:

$$\tau =J{\alpha }_m$$

In SI units, torque is in newton-meters, moment of inertia in kilogram-meters squared ($\text{kg}\cdot {\text{m}}^2$) and angular acceleration in radians per second squared ($\text{rad}/{\text{s}}^2$). Moment of inertia of a rotating object depends on its material and mechanical properties (shape and dimensions).

Work and Power

In linear motion, work $W$ in joules ($\text{J}$), done by a constant force $F$ on an object through a distance $r$ is:

$$W=Fr$$

In rotational motion, work $W$ in joules, done by a constant torque $\tau$ on an object through an angle m is:

$$W=\tau {\theta }_m$$

Power, in joules per second $(J/s)$ or watts ($W$), is defined as the rate of change of work with respect to time. In linear motion, this is:

$$P=\frac{dW}{dt}=\frac{d(Fr)}{dt}=F\frac{dr}{dt}=Fv$$

The force F has been assumed constant.

In rotational motion, the above becomes:

$$P_m=\frac{dW}{dt}=\frac{d(\tau {\theta }_m)}{dt}=\tau \frac{d{\theta }_m}{dt}=\tau {\omega }_m$$

The torque $\tau$ has been assumed constant. Equation is of special importance in the analysis, design, control, and operation of electric machines.

Kinetic Energy

In linear motion, the kinetic energy of a moving object, in joules, is related to its mass and velocity as:

$$E_k=\frac{1}{2}m{v}^2$$

In rotational motion, the kinetic energy of a rotating object, in joules, is related to its moment of inertia and angular velocity as:

$$E_k=\frac{1}{2}J{\omega }_m^2$$