Unit impulse

Definition

Unit impulse refers to a Dirac delta function defined as:

$$\begin{array}{r}\delta (t)=0\text{ for }t\ne 0\\ {\int }_{-\infty }^{\infty }\delta (t)dt=1\end{array}$$

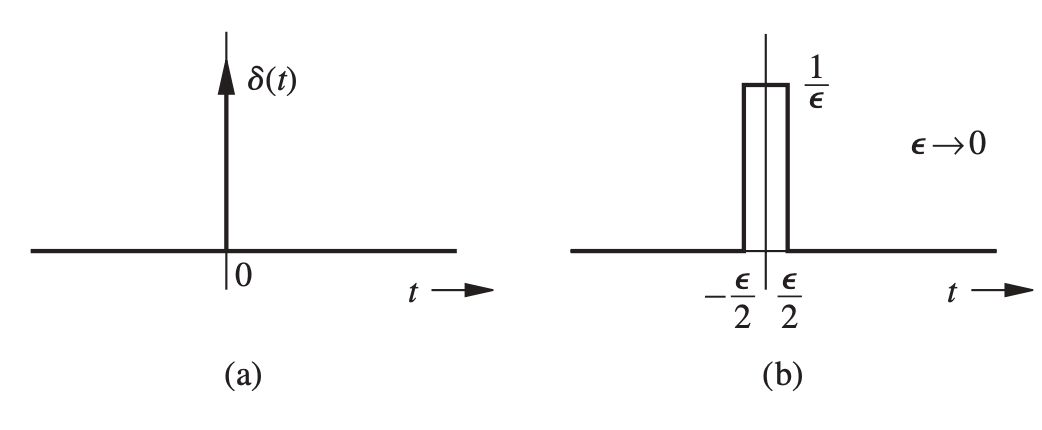
Basically, it has:

• Infinitesimally small width ($ϵ\to 0$)
• Infinitely large height ($\frac{1}{ϵ}\to \infty$)
• Overall area of unity ($1$) Other pulses (rectangular, triangular, Gaussian) can also be used to model impulses.

Properties

Multiplication

Provided a signal $\varphi (t)$ at time $t=T$, multiplying it by an impulse $\delta (t-T)$ results in an impulse located at $t=T$ with amplitude/strength $\varphi (T)$ (value of $\varphi (t)$ at the location of the impulse).

$$\varphi (t)\delta (t-T)=\varphi (T)\delta (t-T)$$

Sampling/sifting

From the above equation, we also have:

$$\begin{array}{rl}{\int }_{-\infty }^{\infty }\varphi (t)\delta (t-T)dt& =\varphi (t){\int }_{-\infty }^{\infty }\delta (t)dt\\ & =\varphi (T)\end{array}$$

This means that the area under the product of a function with an impulse $\delta (t-T)$ is equal to the value of that function at the instant at which the unit impulse is located.

Relationship with Unit Step Function

Because the Unit step function is discontinuous at $t=0$, its derivative does not exist there in the normal sense. But, we actually have:

$$\begin{array}{rl}{\int }_{t_0}^{t_1}\frac{du}{dt}dt& =u(t_1)-u(t_0)\text{for }{t}_0<0<t_1\\ & =1-0=1\end{array}$$ $${\int }_{-\infty }^{\infty }\frac{du}{dt}dt=u(\infty )-u(-\infty )=1$$

Therefore,

$$\frac{du(t)}{dt}=\delta (t)$$

Textbook explanation:

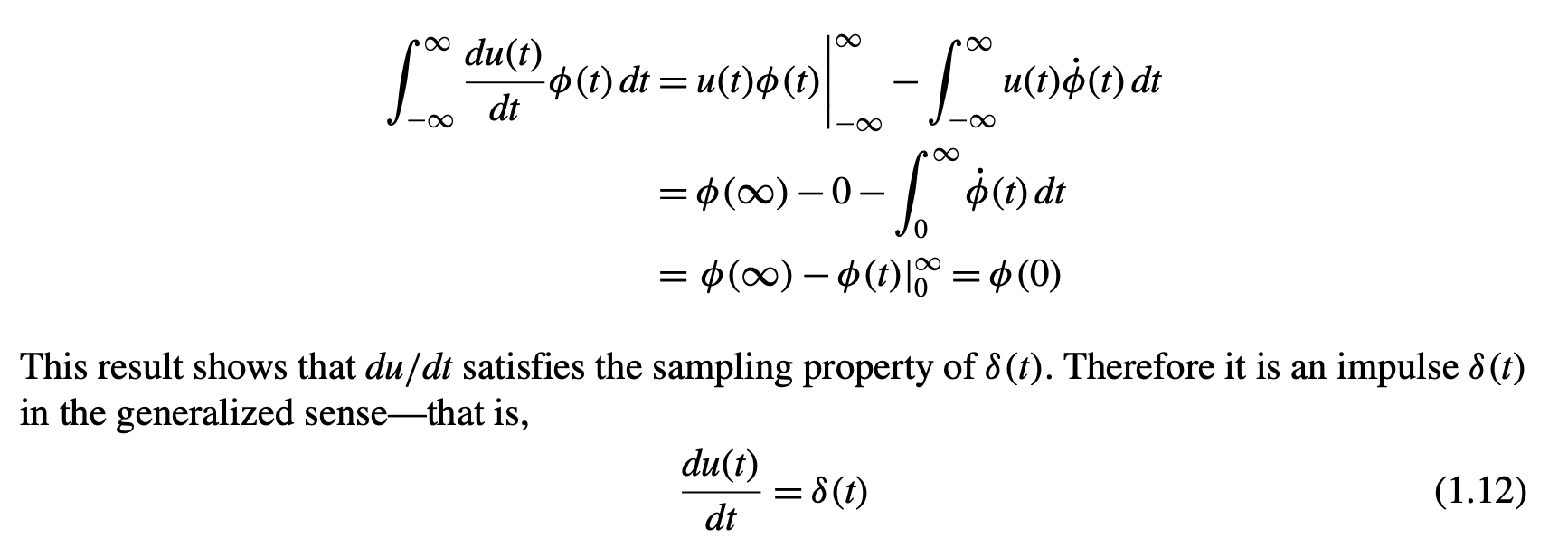
Not really sure why this is useful but it’s pretty interesting?