Task 4: Programming Bandpass Filter Bank
Our bandpass filter is designed to be flexible between IIR and FIR filter types, so that the two can be easily compared. We implemented normalization to ensure the filter frequencies are within the valid range, avoiding issues at the boundaries, and provided a flexible structure to switch between filter types as needed.
### Bandpass Filter
### FIR filter is used because it is linear phase and stable but may require higher filter order
### IIR filter are more computationally efficient (lower order for the same performance) but can have nonlinear phase responses, which might affect the signal.
def create_bandpass_filter(frequencies, samplerate, filter_type='IIR', order=4):
low, high = frequencies
nyquist = 0.5 * samplerate
# Avoid boundaries to avoid issues
low_normalized = max(min(low / nyquist, 0.99), 0.01)
high_normalized = max(min(high / nyquist, 0.99), 0.01)
if filter_type == 'IIR':
b, a = butter(order, [low_normalized, high_normalized], btype='bandpass')
return lambda data: lfilter(b, a, data)
elif filter_type == 'FIR':
# Ensure the frequencies are within the valid range
low = max(low, 1) # Prevent 0 frequency
high = min(high, samplerate / 2 - 1) # Prevent going above Nyquist frequency
b = firwin(order, [low, high], pass_zero=False, fs=samplerate)
return lambda data: np.convolve(data, b, mode='same')Task 5: Programming Bandpass Filter Bank
Number of Channels: We chose to use N = 20 channels for our filter design. Our research indicates that this is a typical number of frequency bands for cochlear implants [1].
Band distribution: The bands in a cochlear implant are distributed logarithmically based on the way human hearing perceives sound frequencies. Human auditory perception is more sensitive to frequency changes at lower frequencies than at higher frequencies [2]; this means that a small change in a low-frequency sound is more easily detected than the same change in a high-frequency sound.
IIR vs. FIR: IIR filters, characterized by feedback components, can achieve a desired filter response with fewer coefficients, making them computationally efficient. However, they can have non-linear phase responses which may distort the signal. On the other hand, FIR filters operate without feedback, using a finite number of coefficients. This gives them a , which is particularly advantageous in applications like cochlear implants where phase alignment is critical for signal interpretation.
We choose to use an FIR filter in our design. The linear phase response of FIR filters is crucial for maintaining the temporal cues of speech, which are essential for users to understand spoken language through a cochlear implant. These filters ensure that all frequencies are delayed by the same amount, preserving the waveform’s shape and avoiding phase distortion, which can be critical for the accurate perception of complex sounds. Despite FIR filters typically requiring more computational resources, the benefits they offer in preserving signal integrity align closely with the auditory requirements of cochlear implant users.
# Filter the sound with the passband bank
N = 20
bands = define_frequency_bands(N)
filtered_signals = [create_bandpass_filter(band, samplerate, filter_type='FIR')(data) for band in bands]Task 6: Plot the output signals of the lowest and highest frequency channels
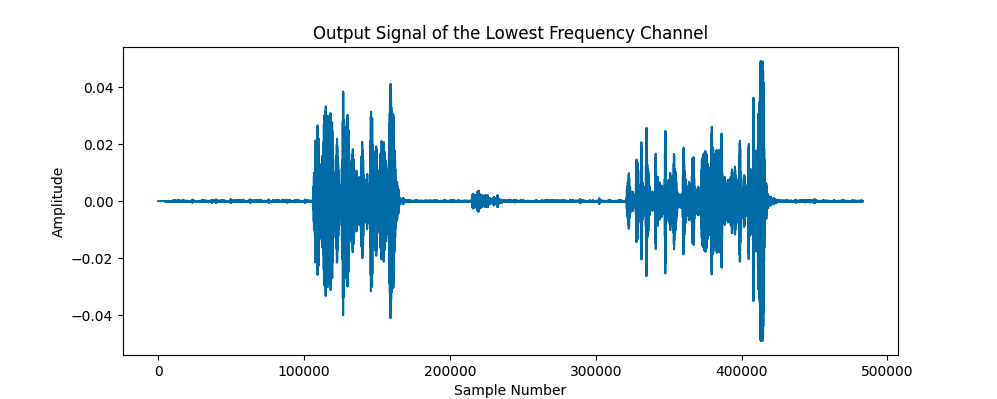
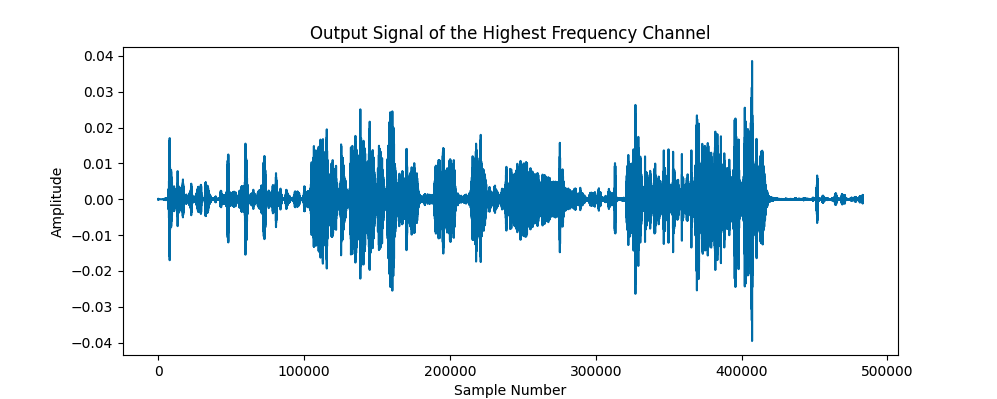
Task 7: Rectify the output signals of all bandpass filters.
The signal is rectified by taking the absolute value.
### Rectify by taking absolute value
def rectify_signal(signal):
return np.abs(signal)Task 8: Detect the envelopes of all rectified signals using a lowpass filter with 400Hz cutoff.
The create_lowpass_filter function sets up a low-pass filter, essential for smoothing the rectified signal to extract its envelope. To achieve a smoother envelope, we use a higher order FIR filter and the Hamming window. The filtfilt function is used to apply this filter in a zero-phase manner, avoiding any time shifts in the signal that could distort the envelope.
The extract_envelope function combines the rectification ripples step and the low-pass filter. The resultant signal is a smooth representation of the original signal’s amplitude variations, or envelope, which is vital in cochlear implants to convey the intensity patterns of sounds to the user without the fine temporal details that cannot be resolved by the device.
### Lowpass filter
def create_lowpass_filter(cutoff, samplerate, filter_type='FIR', order=100):
# Normalized cutoff frequency
normalized_cutoff = cutoff / (0.5 * samplerate)
if filter_type == 'FIR':
# Pass a string or tuple for the window type directly to firwin
b = firwin(order+1, normalized_cutoff, window='hamming', pass_zero='lowpass', fs=samplerate)
# Use filtfilt to apply the filter forward and backward
return lambda data: filtfilt(b, [1], data)
else:
# Implementation for IIR filter if needed
b, a = butter(order, normalized_cutoff, btype='low')
return lambda data: filtfilt(b, a, data)
def extract_envelope(signal, samplerate, filter_type='FIR', order=100):
rectified_signal = np.abs(signal) # Ensure rectification is correct
lowpass_filter = create_lowpass_filter(400, samplerate, filter_type, order)
return lowpass_filter(rectified_signal)Task 9: Plot the extracted envelope of the lowest and highest frequency channels
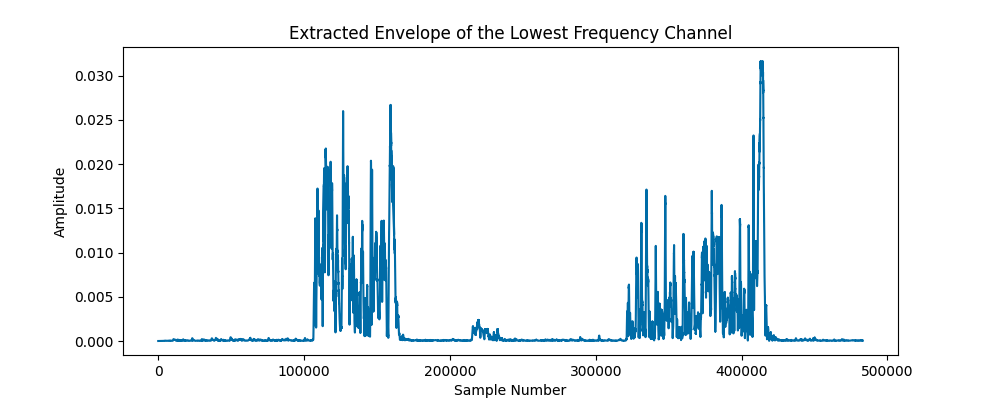
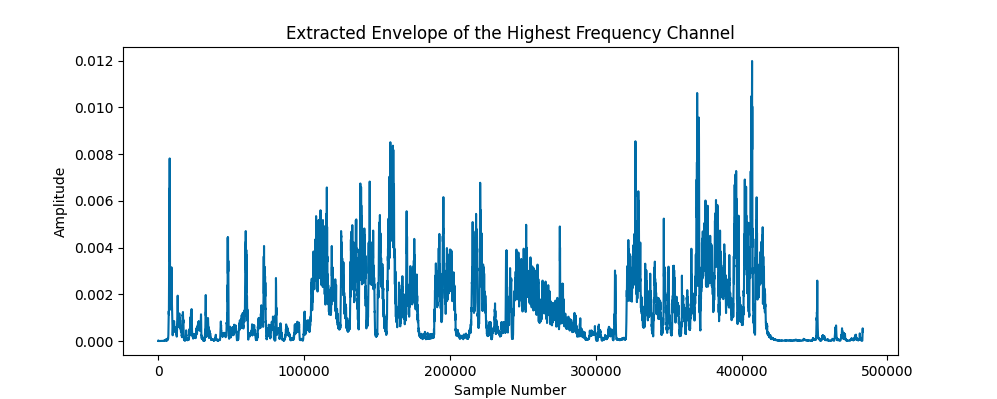
References
[1] Bosen AK, Chatterjee M. Band importance functions of listeners with cochlear implants using clinical maps. J Acoust Soc Am. 2016 Nov;140(5):3718. doi: 10.1121/1.4967298. PMID: 27908046; PMCID: PMC5392084.
[2] Dr. Ir. S. Pigeon, “The non-linearities of the human ear,” Free Online Audio Tests, Test Tones and Tone Generators, https://www.audiocheck.net/soundtests_nonlinear.php.