Signals in Different Domains

Time

In the time domain, the signal varies as a function of time.

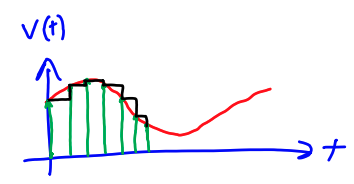
$V(t)$ is specified at every instantaneous $t$. It is composed of an infinite number of $\delta$ functions.

Fourier

The Fourier (frequency) domain composes the signal using a sum of sinusoids.

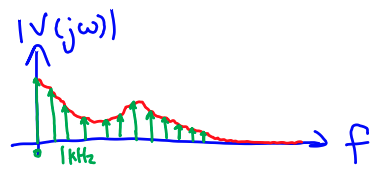
$|V(j\omega )|$ is a continuous spectrum of sinusoids specified at every $f$. At a given $f_0$, $V(j\omega )$ specifies the magnitude and phase as a complex number. This turns calculus in the time domain to complex algebra.

Laplace

In the Laplace domain, basis functions are a mix of time and frequency.

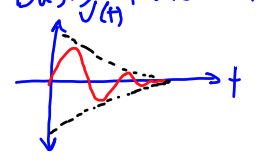
The basis functions is a sine wave, but it’s amplitude is modulated by an envelope because we want to restrict it in time:

$$e^{st}=e^{\alpha t}{e}^{j\omega t}$$

where $e^{\alpha t}$ is an envelope and $e^{j\omega t}$ is a sinusoid.

Example

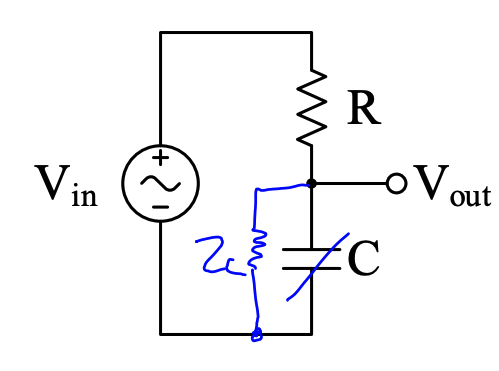
We use $s$ instead of $j\omega$, such that:

$$Z_c=\frac{1}{sC}$$

Then, as a voltage divider, we would have:

$$\begin{array}{rl}{V}_{out}& =V_{in}\times \frac{Z_c}{Z_c+R}\\ & =V_{in}\times \frac{\frac{1}{sC}}{\frac{1}{sC}+R}\times \frac{sC}{sC}\\ & =V_{in}\times \left(\frac{1}{1+sRC}\right)\end{array}$$