Bode Plots

Bode plots show the frequency response of a transfer function. Consider:

$$A(s)=\frac{sL}{sL+R}=\frac{s\frac{L}{R}}{s\frac{L}{R}+1}=\frac{s{\tau }_0}{s{\tau }_0+1}=\frac{\frac{s}{{\omega }_c}}{\frac{s}{{\omega }_c}+1}$$

This is the high-pass filter example from Circuit to Transfer Function.

We plot the Bode Magnitude Plot $|A(s)|$ and the Bode Phase Plot $|\angle A(s)|$.

Bode Magnitude Plot

Here, we substitute $s=j\omega$ back in to sweep frequency.

$$A(j\omega )=\frac{j\omega /{\omega }_c}{j\omega /{\omega }_c+1}$$

• At low frequency, $|A|\to 0$ (negative dB)
• At high frequency, $|A|\to 1$ (0 dB)
• For ${\omega }_c$ we know that $|A|=\frac{1}{\sqrt{2}}$ (-3 dB)

As $\omega$ decreases away from ${\omega }_c$, what happens to $|A|$? Imagine we have $\frac{x}{x+1}$. This looks like $\frac{x}{1}$ at small frequencies. So, if $\omega$ decreases by $10\times$, then $|A|$ decreases by $10\times$ (20dB). This tells us the slope of the plot

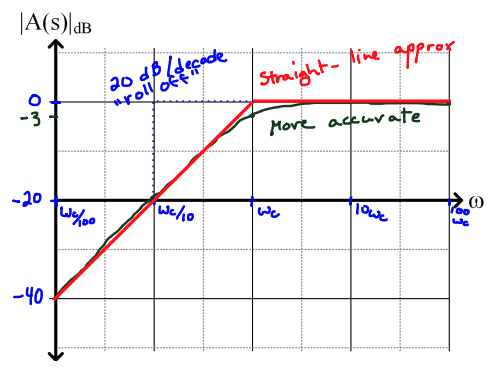
• Red: Bode Straight-Line approximation
• Green: More accurate

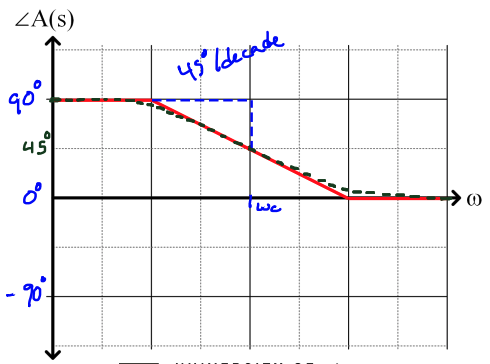
Bode Phase Plot

For $\angle A$, we have:

$$\angle A=\angle N-\angle D$$

where N and D are the numerator and denominator. Since $N=j\omega /{\omega }_c$ has no real component, it is always $90°$.

On the other hand:

• $\angle D$ at low frequency approaches $0°$ (value of $1$), $\angle A=90°$
• $\angle D$ at high frequency approaches $90°$ (value of $j$), $\angle A=0°$
• $\angle D$ at ${\omega }_c$ approaches $45°$ (value of $j+1$), $\angle A=45°$