Shooting Method

The shooting method treats a BVP problem as an initial condition problem. Reduce 2nd-order ODE to two 1st-order ODEs.

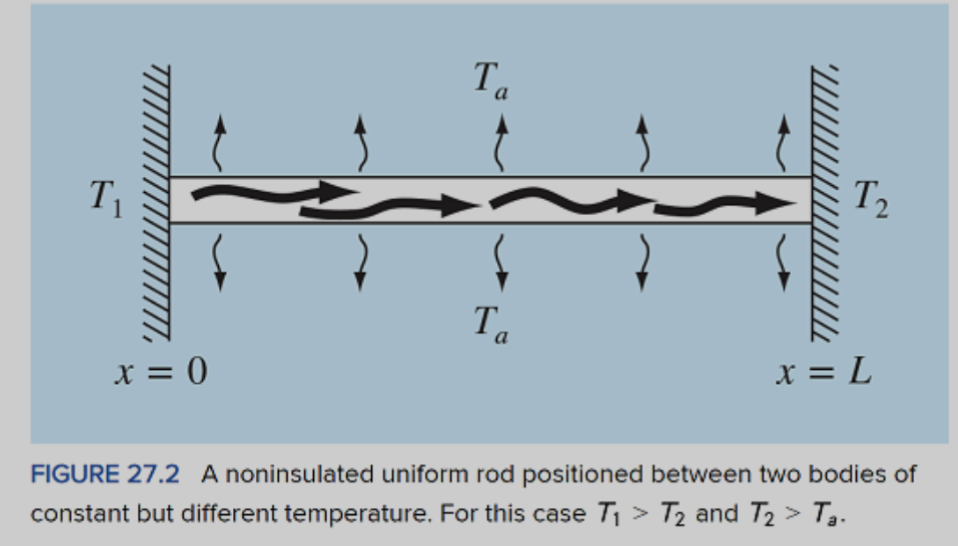
Recall our thermal rod example:

BVP Example

Heat transfer from an uninsulated rod to ambient, with two thermal boundary conditions (one at each end of the rod):

$$\frac{d^{2}T}{d{x}^2}+h^{\prime }(T_a-T)=0$$

With conditions:

$$\begin{array}{r}T(0)=T_1\\ T(L)=T_2\end{array}$$

For $0\le x\le L$, $L=10\text{ m}$:

• $T_a=20$
• $T_1=40$
• $T_2=200$
• $h^{\prime }=0.01$ (Heat coefficient, not step size)

Link to original

We use the substitution method covered in 2nd-order ODEs to convert

$$\frac{d^{2}T}{d{x}^2}+h^{\prime }(T_a-T)=0$$

into two first-order ODEs:

$$\begin{array}{rl}\frac{dT}{dx}& =z\\ \frac{dz}{dx}& =h^{\prime }(T-T_a)\end{array}$$

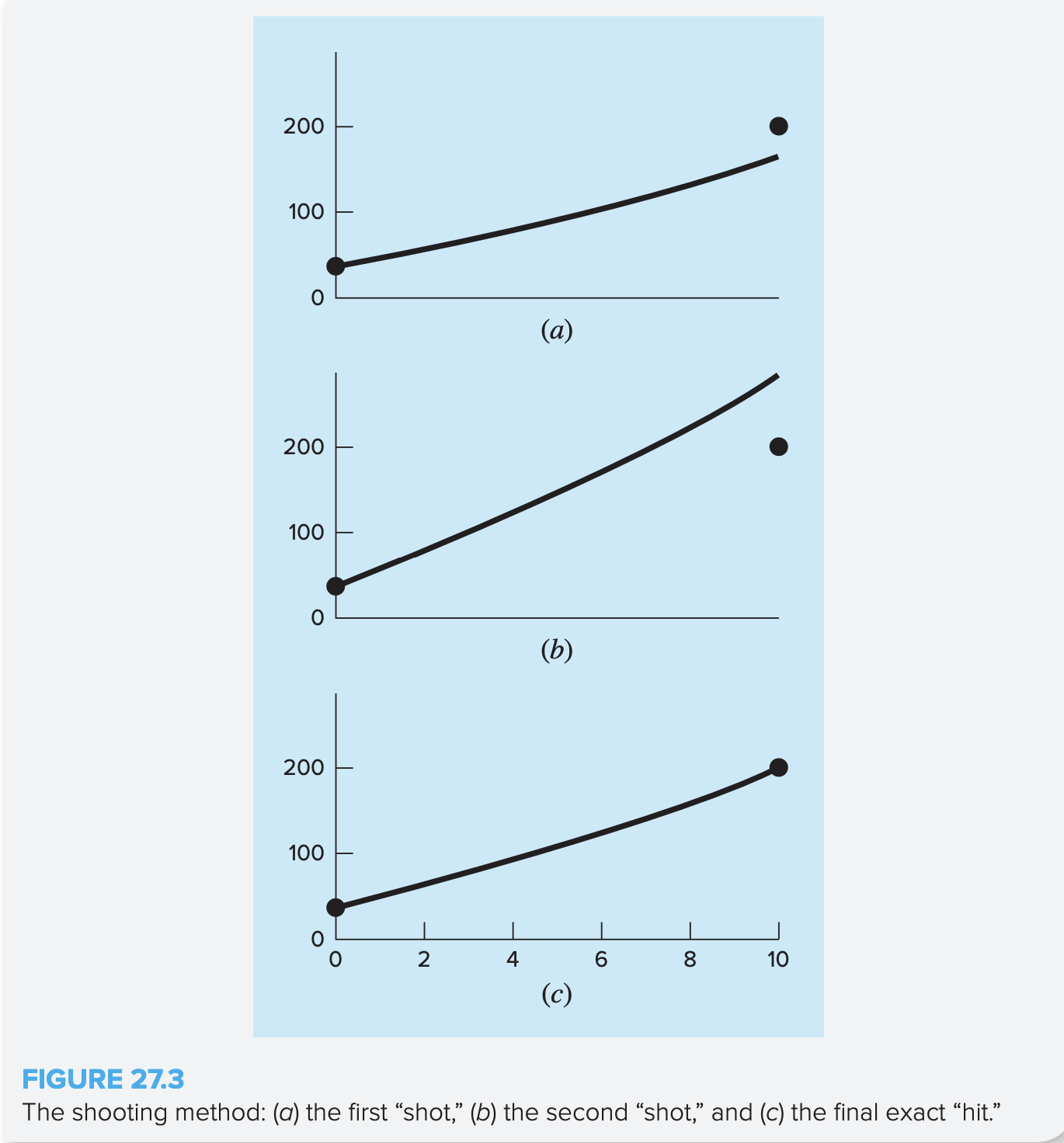
To solve these, we require an initial value for $z$. In this case, we just guess a value, and say $z(0)=10$.

Then, we can solve these equations using a normal method such as Runge-Kutta Method. Using a 4th-order RK method with $h=2$, we get $T(10)=168.3797$.

This doesn’t match the boundary condition of $T(10)=200$, so we guess $z(0)=20$, which gives us $T(10)=285.8980$.

We can interpolate between these to find the right $z(0)$, such that:

$$z(0)=10+\frac{20-10}{285.8980-168.3797}(200-168.3797)=12.6907$$

This value can then be used to determine the correct solution.