MATLAB Worksheet 1

Q1

1a.

$$z=\frac{x^2+e^{0.4y}}{y}+5$$ $$z=\frac{0.5}{xy}$$ $$z=7x^2-18+85y^2$$

1b.

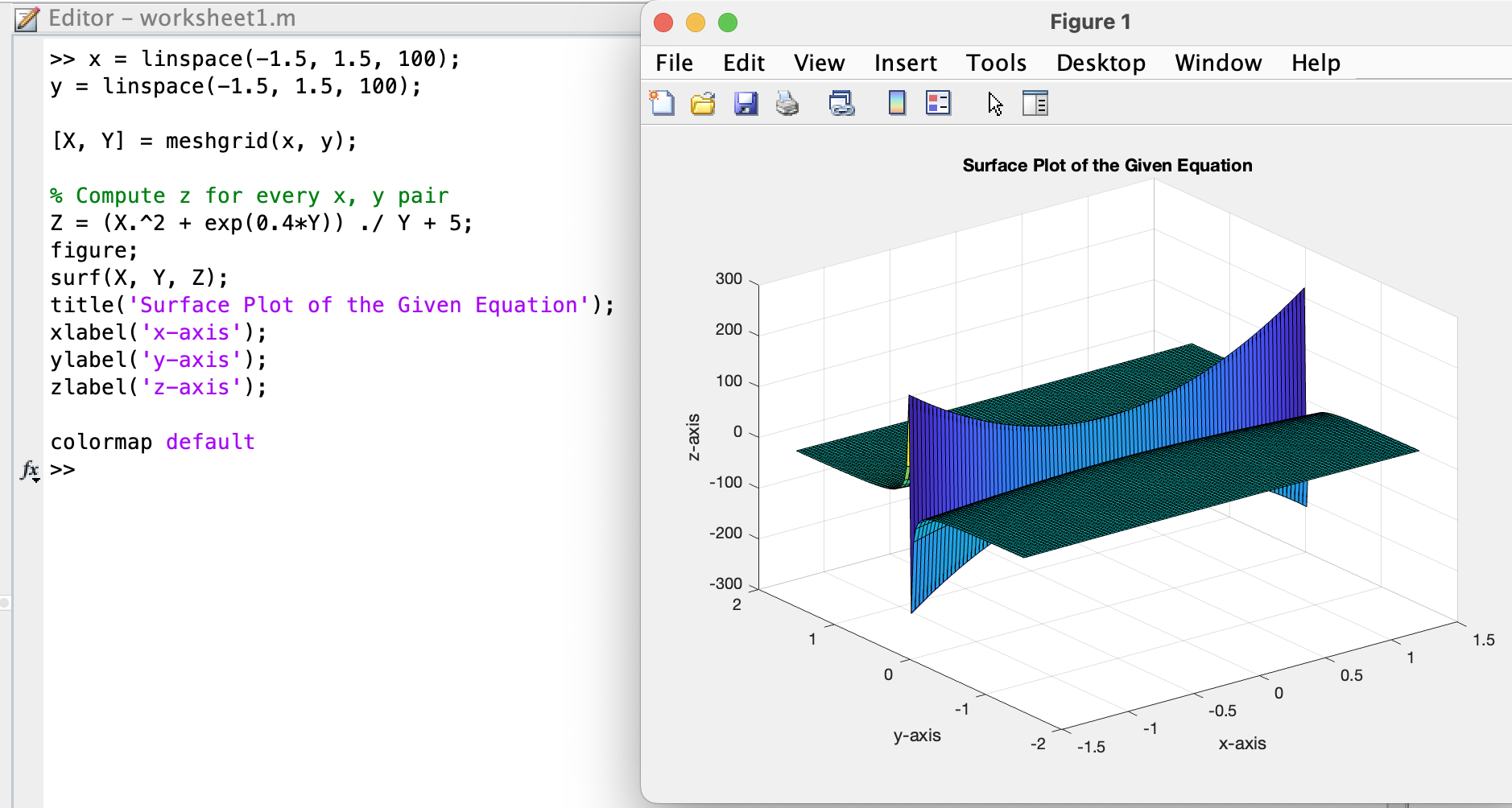
1c.

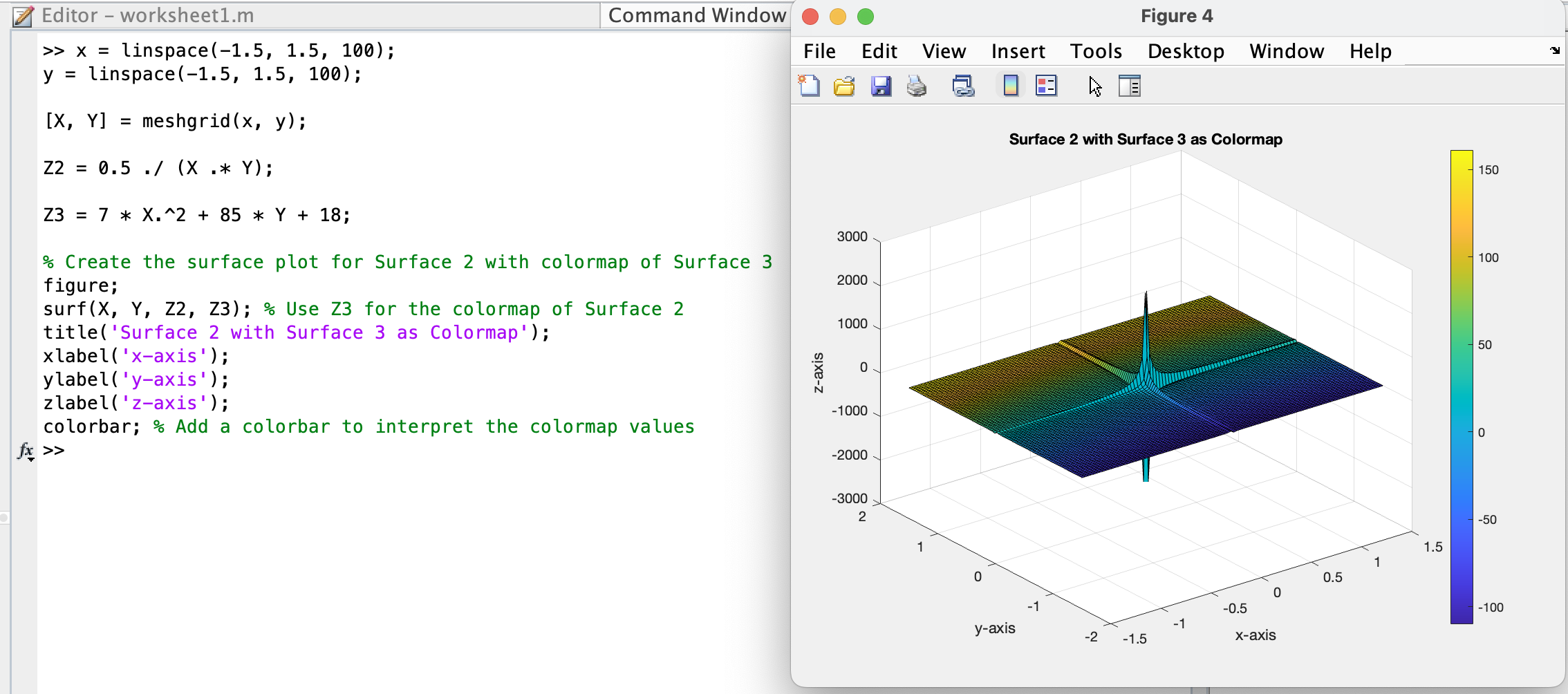
1d.

Equation 1:

$$\begin{array}{r}z=\frac{x^2+e^{0.4y}}{y}+5\\ z-\frac{x^2+e^{0.4y}}{y}-5=0\\ f_1(x,y,z)=zy-x^2-e^{0.4y}-5y=0\end{array}$$

Equation 2:

$$\begin{array}{r}xyz=0.5\\ z=\frac{0.5}{xy}\\ z-\frac{0.5}{xy}=0\\ f_2(x,y,z)=xyz-0.5=0\end{array}$$

Equation 3:

$$\begin{array}{r}7x^2-18=-85y^2+z\\ 7x^2-18+85y^2-z=0\\ f_3(x,y,z)=7x^2-18+85y^2-z\end{array}$$

1e.

function f = equations(v)
    % Extract components of v
    x = v(1);
    y = v(2);
    z = v(3);
 
    % Calculate the values of f1, f2, and f3
    f1 = z*y - exp(0.4*y) - 5*y - x^2;
    f2 = x*y*z - 0.5;
    f3 = z - 7*x^2 - 85*y^2 + 18;
    
    % Combine results into output f
    f = [f1; f2; f3];
end

1f.

Code:

% Main Script
% Define the initial guesses
initial_guess1 = [1, 1, 1];
initial_guess2 = [-1, -1, -1]; % Or any other appropriate guess
 
% Use fsolve to find the solutions
solution1 = fsolve(@equations, initial_guess1);
solution2 = fsolve(@equations, initial_guess2);
 
% Calculate the function values at the found solutions
function_values1 = equations(solution1);
function_values2 = equations(solution2);
 
% Display the solutions and corresponding function values
disp('Solution with initial guess 1:');
disp(['x = ', num2str(solution1(1)), ', y = ', num2str(solution1(2)), ', z = ', num2str(solution1(3))]);
disp(['f1 = ', num2str(function_values1(1)), ', f2 = ', num2str(function_values1(2)), ', f3 = ', num2str(function_values1(3))]);
 
disp('Solution with initial guess 2:');
disp(['x = ', num2str(solution2(1)), ', y = ', num2str(solution2(2)), ', z = ', num2str(solution2(3))]);
disp(['f1 = ', num2str(function_values2(1)), ', f2 = ', num2str(function_values2(2)), ', f3 = ', num2str(function_values2(3))]);
 
% Local function defining the system of equations
function f = equations(v)
    x = v(1);
    y = v(2);
    z = v(3);
 
    f1 = z*y - exp(0.4*y) - 5*y - x^2;
    f2 = x*y*z - 0.5;
    f3 = z - 7*x^2 - 85*y^2 + 18;
    
    f = [f1; f2; f3];
end
 

Output:

Solution with initial guess 1:
x = 0.12558, y = 0.54451, z = 7.3124
f1 = -9.0656e-11, f2 = 2.4131e-10, f3 = -3.7377e-10
Solution with initial guess 2:
x = -0.79461, y = -0.42112, z = 1.4942
f1 = -7.7206e-12, f2 = -6.4525e-12, f3 = -4.5123e-11

Q2

2a.

$$\begin{array}{rl}{z}^2-2\sin (y)x{e}^{-(x^2+y^2)}z+{\sin }^2(y)x^2(e^{-(x^2+y^2)}{)}^2& =0\\ z^2-2e^{-y^2-x^2}xz\sin (y)+e^{-2y^2-2x^2}{x}^2{\sin }^2(y)& =0\\ (z-e^{-y^2-x^2}x\sin (y){)}^2& =0\\ z=f(x,y)& =e^{-y^2-x^2}x\sin (y)\end{array}$$

2b.

Substituting $y=x$ into $z=f(x,y)$:

$$\begin{array}{rl}z& =e^{-x^2-x^2}\cdot x\cdot \sin (x)\\ & =e^{-2x^2}\cdot x\cdot \sin (x)\end{array}$$

In parametric form:

$$\begin{array}{rl}x& =t\\ y& =t\\ z& =e^{-2t^2}\cdot t\cdot \sin (t)\end{array}$$

2c (i).

![[Pasted image 20230921150358.png]]

x = -2:0.1:2;
y = -2:0.1:2;
 
[X, Y] = meshgrid(x, y);
 
Z = exp(-Y.^2 - X.^2) .* X .* sin(Y);
 
figure;
surfc(X, Y, Z);
title('3D Surface with Level Curves');
xlabel('x');
ylabel('y');
zlabel('z');

2c(ii).

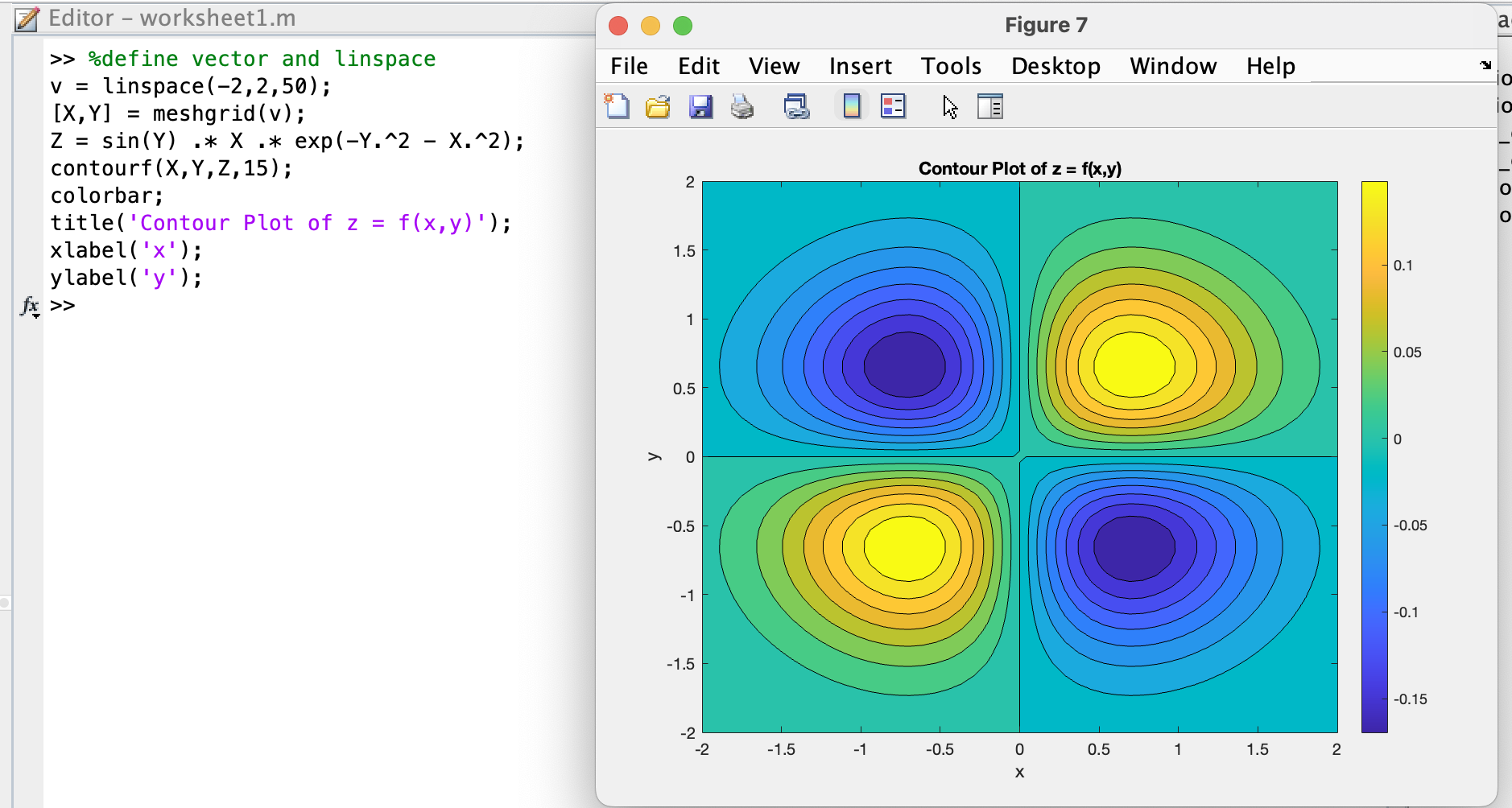
v = linspace(-2,2,50);
[X,Y] = meshgrid(v);
Z = sin(Y) .* X .* exp(-Y.^2-X.^2);
contourf(X,Y,Z,15);
colorbar;
title('Contour Plot of z = f(x,y)');
xlabel('x');
ylabel('y');

2c(iii).

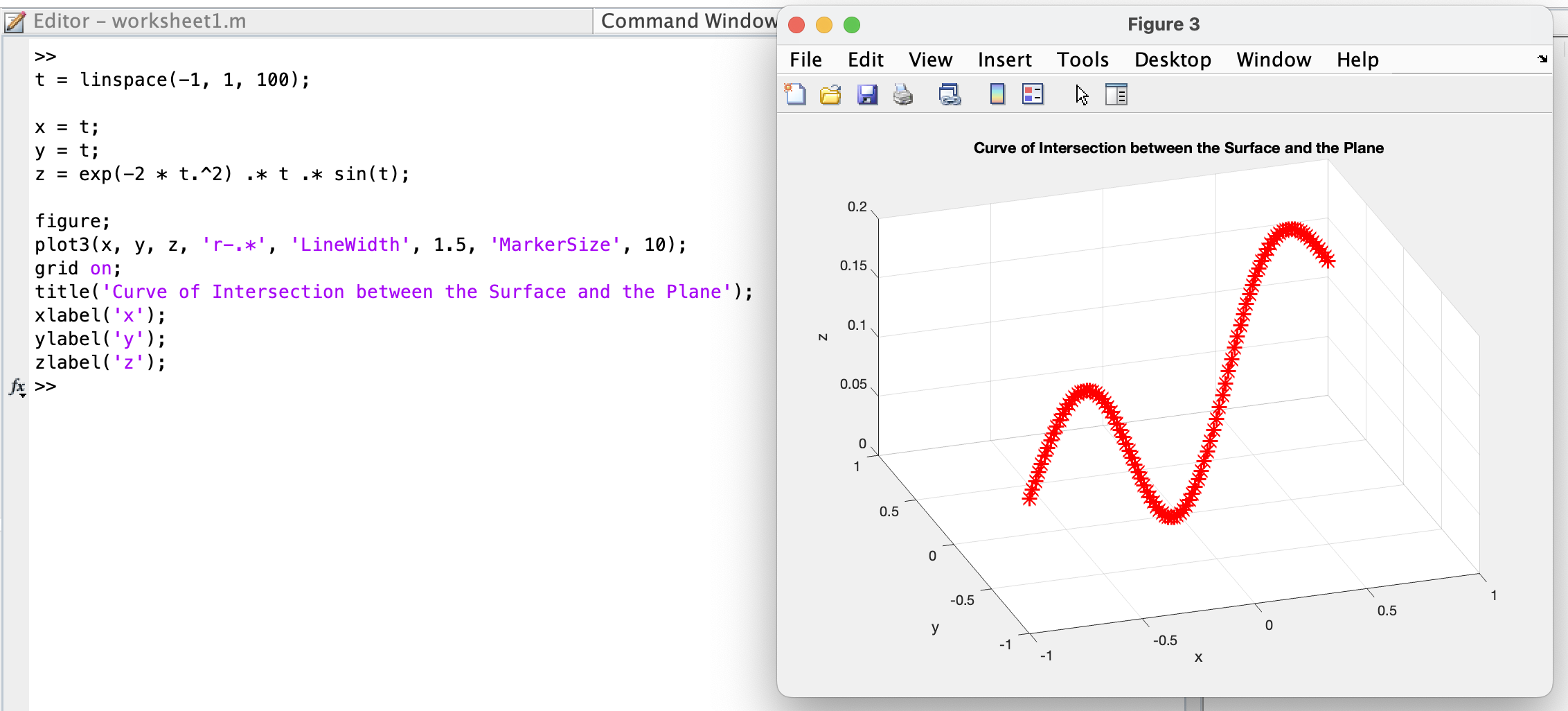
t = linspace(-1, 1, 100);
 
x = t;
y = t;
z = exp(-2 * t.^2) .* t .* sin(t);
 
figure;
plot3(x, y, z, 'r-.*', 'LineWidth', 1.5, 'MarkerSize', 10);
grid on;
title('Curve of Intersection between the Surface and the Plane');
xlabel('x');
ylabel('y');
zlabel('z');