Transformation of Multivariate Distributions

For Transformation of Densities, we found that if we make a change of variables $x=f(y)$ for a density $p_x(x)$, we have:

$$\begin{array}{rl}{p}_y(y)& =p_x(x)\left|\frac{dx}{dy}\right|\\ & =p_x(g(y))\left|\frac{dg}{dy}\right|\end{array}$$

This can be extended to densities defined over multiple variables. Consider a density $p(\mathbf{x})$ over a $D$-dimensional variable $\mathbf{x}=(x_1,\dots ,x_D{)}^T$, that we transform to a new variable $\mathbf{y}=(y_1,\dots ,y_D{)}^T$, where $\mathbf{x}=\mathbf{g}(\mathbf{y})$. Both variables have the same dimensionality.

The transformed density is then given by the generalization of equation (2) in the form:

$$p_{\mathbf{y}}(\mathbf{y})=p_{\mathbf{x}}(\mathbf{x})|\det J|$$

where $\mathbf{J}$ is the Jacobian matrix whose elements are given by the partial derivatives $J_{ij}=\partial g_i/\partial y_j$, such that:

$$\mathbf{J}=\left[\begin{array}{ccc}\frac{\partial g_1}{\partial y_1}& \dots & \frac{\partial g_1}{\partial y_D}\\ ⋮& \ddots & ⋮\\ \frac{\partial g_D}{\partial y_1}& \dots & \frac{\partial g_D}{\partial y_D}\end{array}\right]$$

The absolute value of the determinant of the Jacobian represents the ratio of these volumes and is the same factor that arises when changing variables within an integral. The formula for the Jacobian follows from the fact that the probability mass in region $\Delta \mathbf{x}$ is the same as the probability mass in $\Delta \mathbf{y}$. Once again, we take the modulus to ensure that the density is nonnegative.

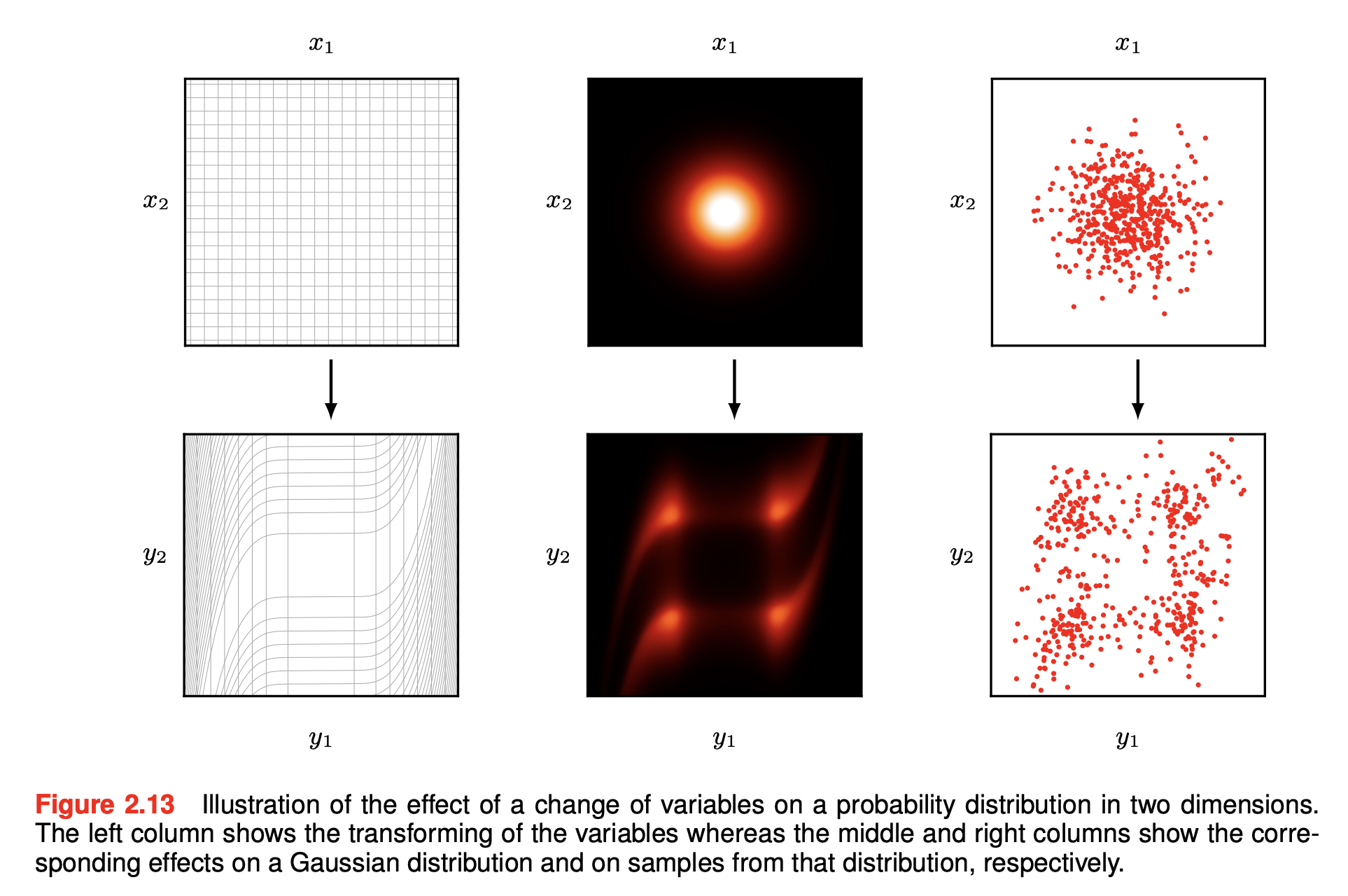
Intuition

Intuitively, we can view the change of variables as expanding some regions of space and contracting others, with an infinitesimal region $\Delta \mathbf{x}$ around a point $\mathbf{x}$ being transformed to a region $\Delta \mathbf{y}$ around the point $\mathbf{y}=\mathbf{g}(\mathbf{x})$.

This illustrated below by applying a change of variables to a Gaussian distribution in 2 dimensions (top row). The transformation from $\mathbf{x}$ to $\mathbf{y}$ is given by:

$$\begin{array}{rl}{y}_1& =x_1+\tanh (5x_1)\\ y_2& =x_2+\tanh (5x_2)+\frac{x_1^3}{3}\end{array}$$

On the bottom row are samples from a Gaussian distribution in $\mathbf{x}$-space along with the corresponding transformed samples in $\mathbf{y}$-space.