Covariance

For two random variables $x$ and $y$, the covariance measures the extent to which the two variables vary together. This is defined by:

$$\begin{array}{rl}\text{cov}[x,y]& =E_{x,y}\left[(x-E[x])(y-E[y])\right]\\ & =E_{x,y}[xy]-E[x]E[y]\end{array}$$

If $x$ and $y$ are independent, then their covariance equals zero.

For two vectors $\mathbf{x}$ and $\mathbf{y}$, their covariance is a matrix given by:

$$\begin{array}{rl}\text{cov}[\mathbf{x},\mathbf{y}]& =E_{\mathbf{x},\mathbf{y}}\left[\{\mathbf{x}-E[\mathbf{x}]\}\{{\mathbf{y}}^T-E[{\mathbf{y}}^T]\}\right]\\ & =E_{\mathbf{x},\mathbf{y}}[{\mathbf{xy}}^T]-E[\mathbf{x}]E[{\mathbf{y}}^T]\end{array}$$

If we consider the covariance of the components of a vector $\mathbf{x}$ with each other, then we use a slightly simpler notation $\text{cov}[x]\equiv \text{cov}[x,x$].

Example

We can consider the covariance to be a measure of the strength of the correlation between two or more sets of random variates.

Assume we have a set of location measurements in the $x$-$y$ plane. Due to the random error, there is a variance in the measurements. Here are the different measurement sets:

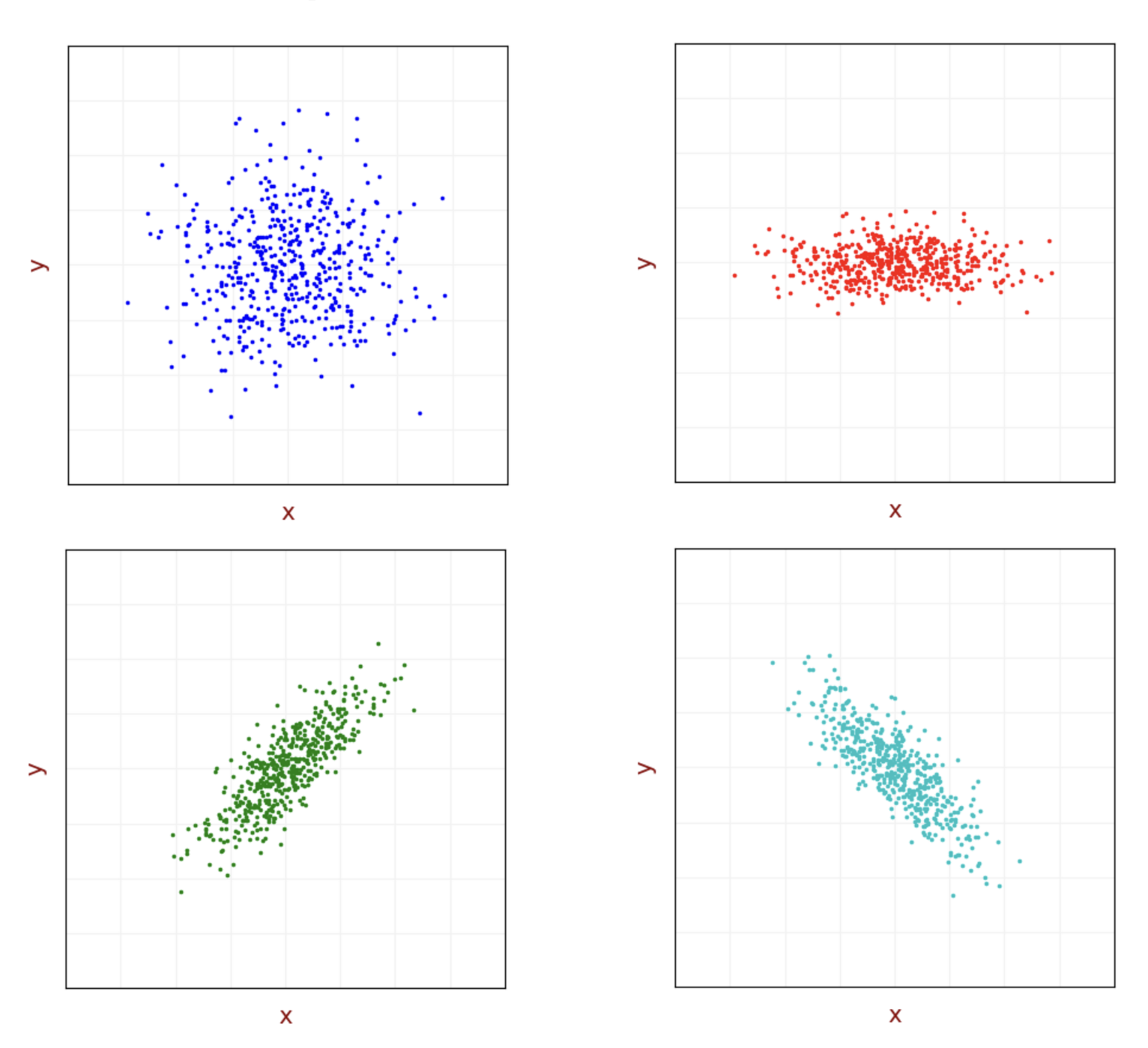
The two upper subplots demonstrate uncorrelated measurements. The $x$ and $y$ values don’t depend on each other.

• For the blue dataset, the $x$ and $y$ values have the same variance – circular shape.
• For the red dataset, the $x$ values have greater variance than the $y$ values – elliptic shape.
• Since the measurements are uncorrelated, the covariance of $x$ and $y$ equals zero.

The two lower subplots demonstrate correlated measurements. There is a dependency between the $x$ and $y$ values.

• For the green data set, an increase in $x$ results in an increase in $y$ and vice versa. The correlation is positive; therefore, the covariance is positive.
• For the cyan data set, an increase in $x$ results in a decrease in $y$ and vice versa. The correlation is negative; therefore, the covariance is negative.