Confidence Interval

A confidence interval specifies the probability that a parameter falls between a pair of values around the mean for the univariate normal distribution.

For the univariate normal distribution, the area between the $1\sigma$ boundaries and the Gaussian function is 68.26% of the total area under the Gaussian function.

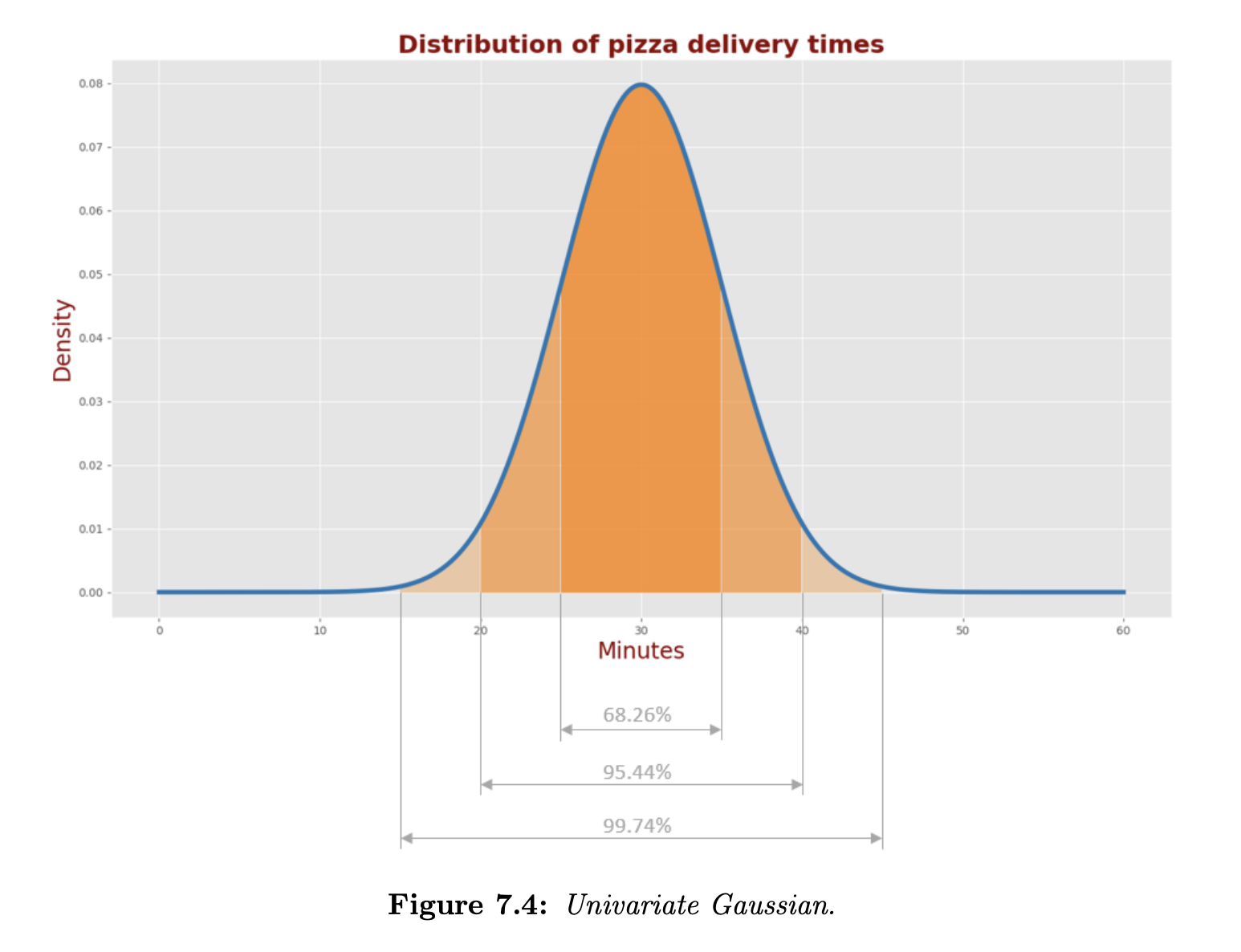
• The confidence interval for the probability of 68.26% is $1\sigma$.
• The confidence interval for the probability of 95.44% is $2\sigma$.
• The confidence interval for the probability of 99.74% is $3\sigma$.

The probability of the bivariate distribution is a volume of the 3-dimensional Gaussian function. For example, the volume of the the 3-dimensional Gaussian function sliced at the $1\sigma$ level is 39.35% of the 3-dimensional Gaussian function.