Kalman Gain Intuition

Recall the basic state update equation. We can re-write it in a form to emphasize its role in weighing the previous estimate and the current measurement:

$$\begin{array}{rl}{\hat{x}}_{n,n}& ={\hat{x}}_{n,n-1}+K_n(z_n-{\hat{x}}_{n,n-1})\\ & =(1-K_n){\hat{x}}_{n,n-1}+K_n{z}_n\end{array}$$

As we can see from above, the Kalman Gain $K_n$ is the measurement weight, and the $(1-K_n)$ is the weight of the current state estimate.

Recall that $K_n$ is calculated as:

$$\begin{array}{rl}{K}_n& =\frac{p_{n,n-1}}{r_n+p_{n,n-1}}\\ & =\frac{\text{Variance in estimate}}{\text{Variance in measurement}+\text{Variance in estimate}}\end{array}$$

Thus, $K_n$ is close to zero when the measurement uncertainty is high and the estimate uncertainty is low. Hence we give a significant weight to the estimate and a small weight to the measurement.

On the other hand, when the measurement uncertainty is low, and the estimate uncertainty is high, $K_n$ is close to one. Hence we give a low weight to the estimate and a significant weight to the measurement.

If the measurement uncertainty equals the estimate uncertainty, then $K_n=0.5$. The Kalman Gain defines the measurement’s weight and the prior estimate’s weight when forming a new estimate. It tells us how much the measurement changes the estimate.

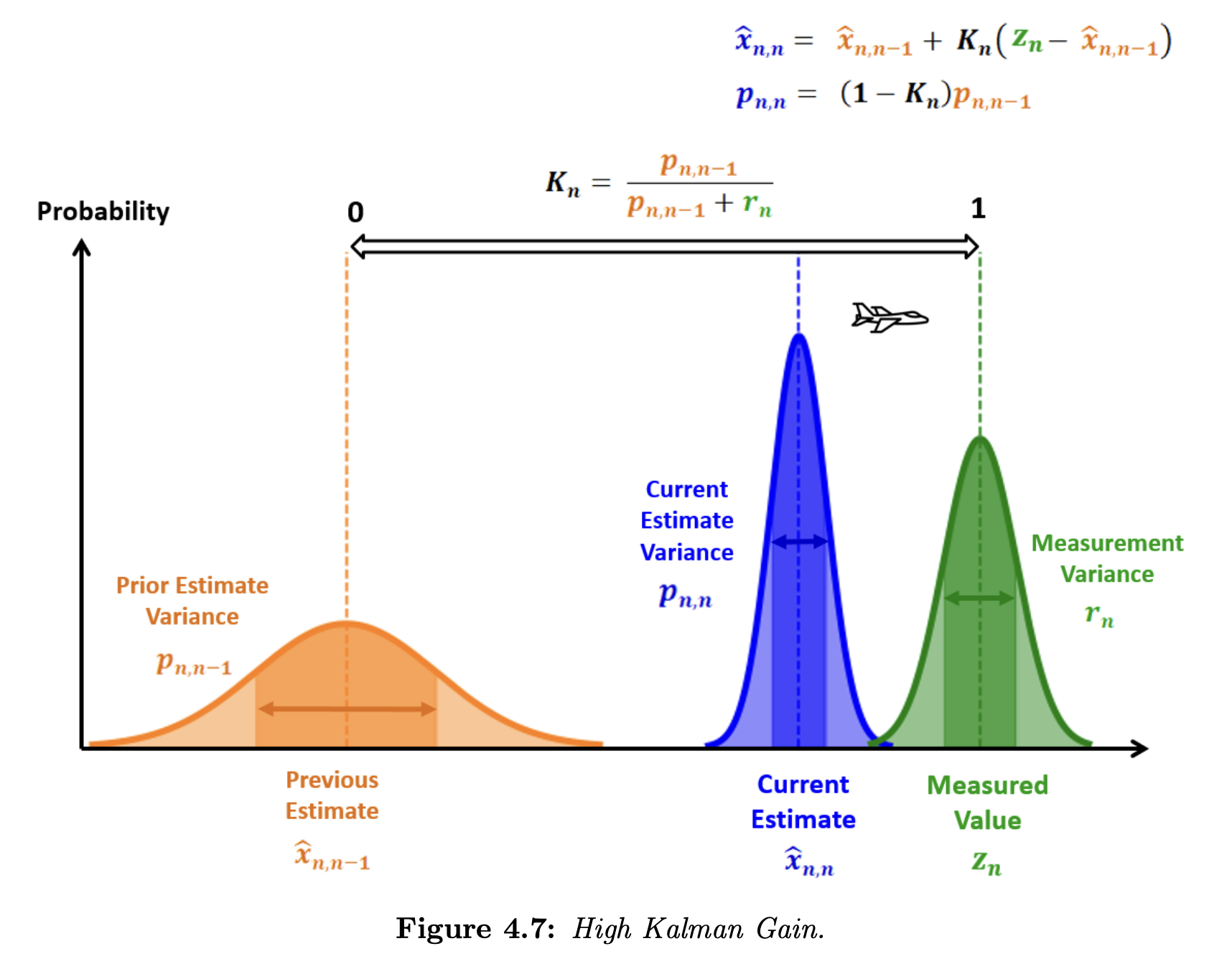
High Kalman Gain

A low measurement uncertainty relative to the estimate uncertainty would result in a high Kalman Gain (close to 1). Therefore the new estimate would be close to the measurement. The following figure illustrates the influence of a high Kalman Gain on the estimate in an aircraft tracking application.

Low Kalman Gain

A high measurement uncertainty relative to the estimate uncertainty would result in a low Kalman Gain (close to 0). Therefore the new estimate would be close to the prior estimate. The following figure illustrates the influence of a low Kalman Gain on the estimate in an aircraft tracking application.