Multi-class Classification

The goal of multi-class is to assign an input data example $\mathbf{x}$ to one of $K>2$ classes, so $y\in \{1,2,\dots ,K\}$.

Examples:

• Predicting which of $K=10$ digits $y$ is present in an image of a handwritten number
• Predicting which of $K$ possible words $y$ follows an incomplete sentence $\mathbf{x}$

Following the loss function recipe, we first choose a distribution over the prediction space $y$. In this case, we have $y\in \{1,2,\dots ,K\}$, so we choose the categorical distribution, which is defined on this domain. This has $K$ parameters ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_K$, which determine the probability of each category:

$$Pr(y=k)={\lambda }_k$$

• Constraints: Each $\lambda$ is in the range $[0,1]$ and they sum to $1$.

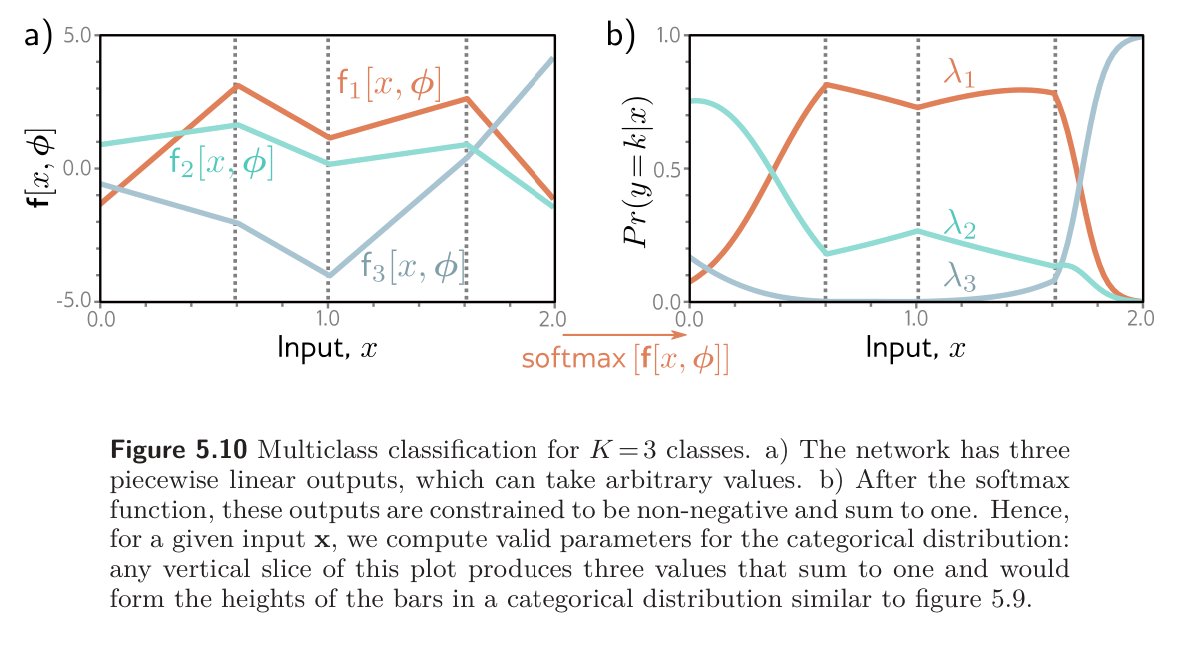
Then, we use a network $f[\mathbf{x},\varphi ]$ with $K$ outputs to compute these $K$ parameters from input $\mathbf{x}$. Unfortunately, the network outputs do not necessarily obey the aforementioned constraints; thus, we pass them through a function that ensures these constraints are respected. This is usually a softmax function.

The softmax takes an arbitrary vector of length $K$ and returns a vector of the same length but where the elements are now in the range $[0,1]$ and sum to $1$. The $k$-th output of the softmax function is

$${\text{softmax}}_k[\mathbf{z}]=\frac{\exp [z_k]}{{\sum }_{k^{\prime }=1}^K\exp [z_{k^{\prime }}]}$$

where the exponential functions ensure positivity, and the sum in the denominator ensures that the $K$ numbers sum to one.

The likelihood that input $\mathbf{x}$ has label $y=k$ is hence:

$$Pr(y=k|\mathbf{x})={\text{softmax}}_k[f[\mathbf{x},\varphi ]]$$

The loss function is the negative log-likelihood of the training data:

$$\begin{array}{rl}L[\varphi ]& =-\sum _{i=1}^I\log \left[{\text{softmax}}_{y_i}\right[f[{\mathbf{x}}_{\mathbf{i}},\varphi ]\left]\right]\\ & =-\sum _{i=1}^I\left(f_{y_i}[{\mathbf{x}}_i,\varphi ]-\log \left[\sum _{k^{\prime }=1}^K\exp [f_{k^{\prime }}[{\mathbf{x}}_i,\varphi ]]\right]\right)\end{array}$$

where $f_{y_i}[\mathbf{x},\varphi ]$ and $f_{k^{\prime }}[\mathbf{x},\varphi ]$ denote the $y_i$-th and $k^{\prime }$-th outputs of the network respectively. This is called multiclass cross-entropy loss.

The transformed model output represents a categorical distribution over possible classes $y\in \{1,2,\dots ,K\}$. For a point estimate, we take the most probable category $\hat{y}=\underset{x}{\mathrm{argmax}}[Pr(y=k|\mathbf{f}[\mathbf{x},\hat{\varphi }])]$. This corresponds to whichever curve is highest for that value of $\mathbf{x}$ in the figure below.