Explicit Regularization

Consider fitting a model $\mathbf{f}[\mathbf{x},\varphi ]$ with parameters $\varphi$ using a training set $\{{\mathbf{x}}_i,{\mathbf{y}}_i\}$ of input/output pairs. We seek the parameters $\hat{\varphi }$ that minimize the loss function $L[\varphi ]$:

$$\begin{array}{rl}\hat{\varphi }& =\underset{\varphi }{\mathrm{argmin}}[L[\varphi ]]\\ & =\underset{\varphi }{\mathrm{argmin}}\left[\sum _{i=1}^I{\ell }_i[{\mathbf{x}}_i,{\mathbf{y}}_i]\right]\end{array}$$

where the individual terms ${\ell }_i[{\mathbf{x}}_i,{\mathbf{y}}_i]$ measure the mismatch between the network predictions $\mathbf{f}[{\mathbf{x}}_i,\varphi ]$ and output targets ${\mathbf{y}}_i$ for each training pair. To bias this minimization toward certain solutions:

$$\hat{\varphi }=\underset{\varphi }{\mathrm{argmin}}\left[\sum _{i=1}^I{\ell }_i[{\mathbf{x}}_i,{\mathbf{y}}_i]+\lambda \cdot g[\varphi ]\right]$$

where:

• $g[\varphi ]$ is a function that returns a scalar which takes larger values when the parameters are less preferred.
• $\lambda$ is a positive scalar that controls the relative contribution of the original loss function and the regularization term.

The minima of the regularized loss function usually differ from those in the original, so the procedure converges to different parameter values.

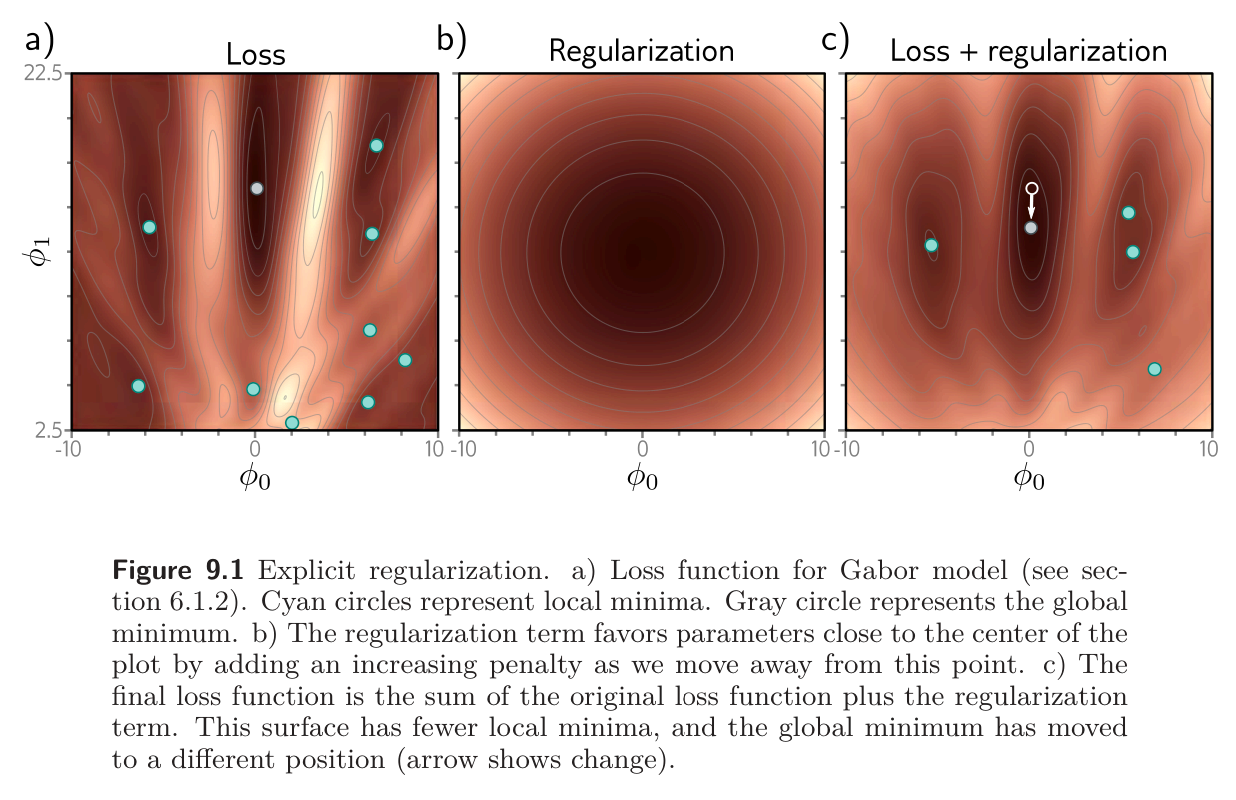
Probabilistic interpretation

Regularization can be viewed from a probabilistic perspective. We’ve seen that loss functions are constructed from the maximum likelihood criterion:

$$\hat{\varphi }=\underset{\varphi }{\mathrm{argmax}}\left[\prod _{i=1}^{I}Pr({\mathbf{y}}_i|{\mathbf{x}}_i,\varphi )\right]$$

The regularization term can be considered a prior $Pr(\varphi )$ that represents knowledge about the parameters before we observe the data. Now, we have a maximum a posteriori or MAP criterion:

$$\hat{\varphi }=\underset{\varphi }{\mathrm{argmax}}\left[\prod _{i=1}^{I}Pr({\mathbf{y}}_i|{\mathbf{x}}_i,\varphi )Pr(\varphi )\right]$$

Moving back to the negative log-likelihood loss function (see loss function recipe) by taking the log and multiplying by $-1$, we see that

$$\lambda \cdot g[\varphi ]=-\log [Pr(\varphi )]$$