Dropout

Dropout is a regularization method that was designed to work with deep neural networks. Rather than perturbing data every time we train (see Weight Perturbation), we’ll perturb the network. This is done randomly; on each training step, selecting a set of units on each layer and prohibiting them from participating. This is done by setting them to zero at each iteration of SGD.

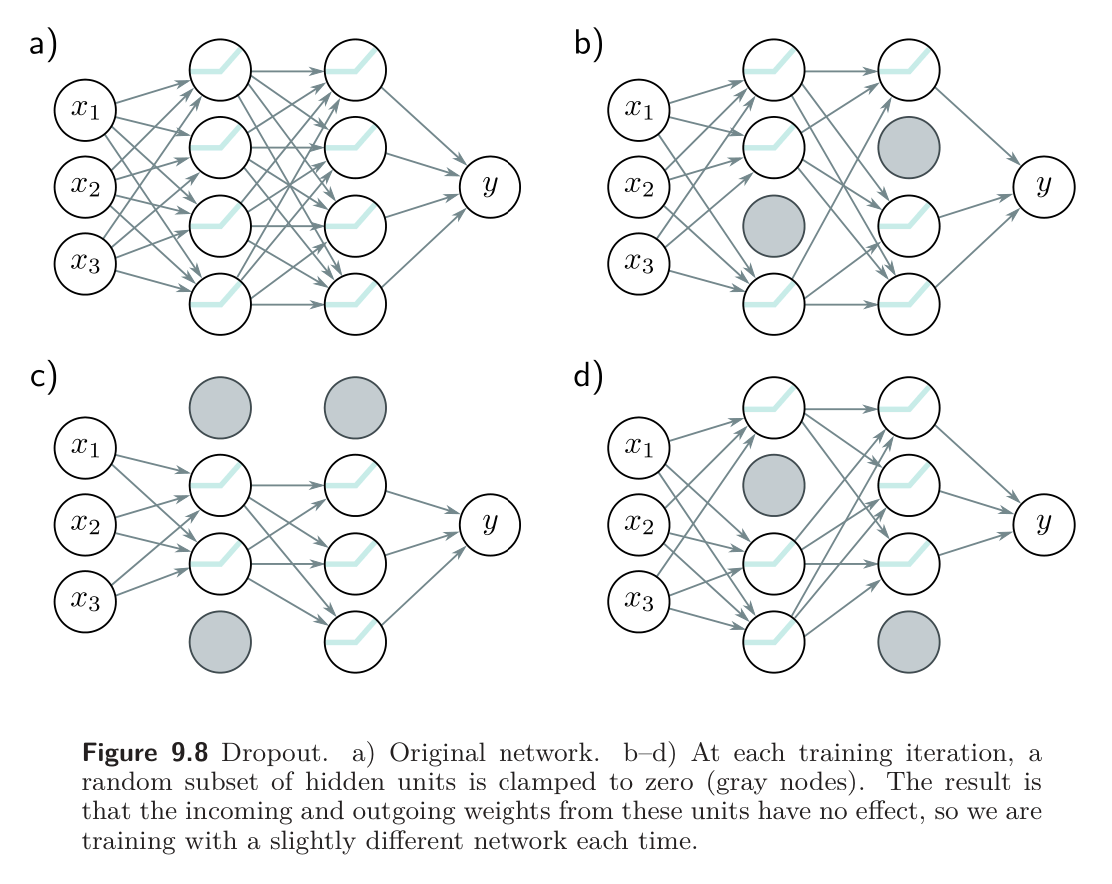
Thus, all of the units will have to take “collective responsibility” of getting the answer right, and the network can’t rely on a small set of weights to do the majority of the computation. Mathematically, this encourages weights to have smaller magnitudes so that the change in the function due to the presence or absence of any specific hidden unit is reduced. This tends also to make the network more robust to data perturbations.

This technique has the positive benefit that it can eliminate undesirable “kinks” in the function that are far from the training data and don’t affect the loss. For example, consider 3 hidden units that become active sequentially as we move along the curve.

• The first hidden unit causes a large increase in the slope.
• The second hidden unit decreases the slope, so the function goes back down.
• The third unit cancels out this decrease and returns the curve to its original trajectory.

When several units conspire like this, eliminating them in dropout causes a considerable change to the output function int he half-space where that unit was active. A subsequent gradient descent step will attempt to compensate for the change that this induces, and such dependencies will be eliminated over time. The overall effect is that large unnecessary changes between training data points are gradually removed even though they contribute nothing to the loss.

Implementation

During the training phase, for each phase, for each training example, for each unit, we randomly set $a_j^l:=0$ with probability $p$. There will be no contribution to the output and no gradient update for the associated unit. When we are done training and want to use the network to make predictions, we multiply all weights by $p$ to achieve the same average activation levels.

Implementing dropout is easy; during the forward pass, we can simply let

$$a^l=f(z^l)\ast d^l$$

where $\ast$ is a element-wise product and $d^l$ is a vector of 0’s and 1’s, drawn randomly with probability $p$. The backwards pass depends on $a^l$ , so we do not need to make any further changes to the algorithm.

$p$ is commonly set to $0.5$, but this is subject to experimentation.

At test time, we can run the network as usual with all the hidden units active; however, the network now has more hidden units than it was trained with at any given probability, so we multiple the weights by $(1-p)$ to compensate. This is known as the weight scaling inference rule.

A different approach to inference is to use Monte Carlo dropout, in which we run the network multiple times with different random subsets of units clamped to zero (as in training) and combine the results. This is closely related to ensembling, as every random version of the network is a different model; however, we do not have to train or store multiple networks here.