Cross-Entropy Loss

Cross-entropy loss is based on the idea of finding parameters $\theta$ that minimize the distance between the empirical distribution $q(y)$ of the observed data $y$ and a model distribution $Pr(y|\theta )$.

The distance between two probability distributions $q(z)$ and $p(z)$ can be evaluated using the Kullback-Leibler Divergence:

$$D_{KL}[q||p]={\int }_{-\infty }^{\infty }q(z)\log [q(z)]dz-{\int }_{-\infty }^{\infty }q(z)\log [p(z)]dz$$

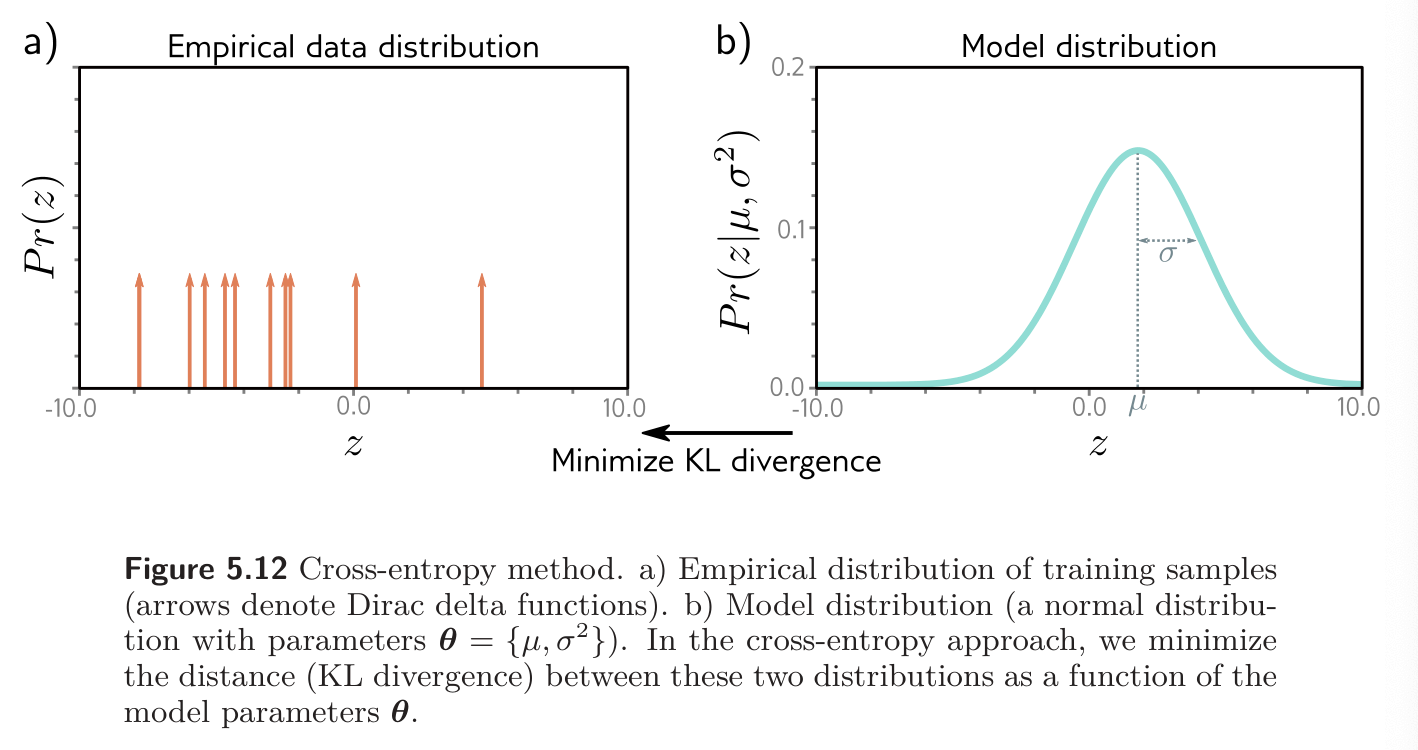
Now consider that we observe an empirical distribution at points $\{y_i{\}}_{i=1}^I$. We can describe this as a weighted sum of point masses:

$$q(y)=\frac{1}{I}\sum _{i=1}^I\delta [y-y_i]$$

where $\delta [\bullet ]$ is the Dirac delta function.

We want to minimize the KL divergence between the model distribution $Pr(y|\theta )$ and this empirical distribution:

$$\begin{array}{rl}\hat{\theta }& =\underset{\theta }{\mathrm{argmin}}\left[{\int }_{-\infty }^{\infty }q(y)\log [q(y)]dy-{\int }_{-\infty }^{\infty }q(y)\log [Pr(y|\theta )]dy\right]\\ & =\underset{\theta }{\mathrm{argmin}}\left[-{\int }_{-\infty }^{\infty }q(y)\log [Pr(y|\theta )]dy\right]\end{array}$$

The first term disappears as it has no dependence on $\theta$. The second term is known as the cross-entropy. It can be interpreted as the amount of uncertainty that remains in one distribution after taking into account what we already know from the other.

Now, we substitute the definition of the empirical distribution $q(y)$:

$$\begin{array}{rl}\hat{\theta }& =\underset{\theta }{\mathrm{argmin}}\left[-{\int }_{-\infty }^{\infty }\left(\frac{1}{I}\sum _{i=1}^I\delta [y-y_i]\right)\log [Pr(y|\theta )]dy\right]\\ & =\underset{\theta }{\mathrm{argmin}}\left[-\frac{1}{I}\sum _{i=1}^I\log [Pr(y_i|\theta )]\right]\\ & =\underset{\theta }{\mathrm{argmin}}\left[-\sum _{i=1}^I\log [Pr(y_i|\theta )]\right]\end{array}$$

The product of the two terms in the first line corresponds to pointwise multiplying the point masses (5.12a) with the logarithm of the distribution (5.12b). We are left with a finite set of weighted probability masses centered on the data points. In the last line, we eliminate the constant scaling factor $1/I$ as this doesn’t affect the position of the minimum.

In machine learning, the distribution parameters are computed by the model $\mathbf{f}[{\mathbf{x}}_i,\varphi ]$, so we have

$$\hat{\varphi }=\underset{\varphi }{\mathrm{argmin}}\left[-\sum _{i=1}^I\log [Pr(y_i|\mathbf{f}[{\mathbf{x}}_i,\varphi ])]\right]$$

This is exactly equivalent to the negative log-likelihood criterion. Cross-entropy and negative log-likelihood are equivalent!