Dropout can be interpreted as applying multiplicative Bernoulli noise to the network activations. This leads to the idea of applying noise to other parts of the network during training to make the final more more robust.
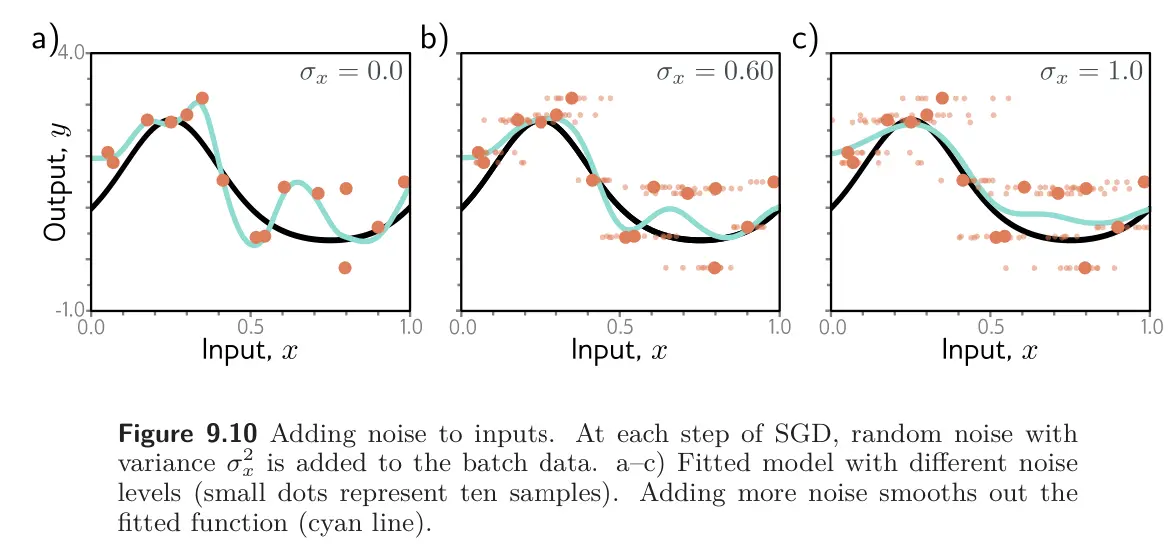
Add noise to input data: This smooths out the learned function. For regression problems, it can be shown (Problem 9.3) to be equivalent to adding a regularizing term that penalizes the network’s output with respect to its input. An extreme version of this is adversarial training.
Add noise to weights: This encourages the network to make sensible predictions for small perturbations of the weights. The results is that the training converges to local minima in the middle of wide, flat regions, where changing the individual weights does not matter much.
Adding noise to labels: The maximum likelihood criterion for multi-class classification aims to predict the correct class with absolute certainty. To this end, the final network activations (i.e. before the softmax) are pushed to very large values for the correct class and very small values for the incorrect class. We could discourage this overconfident behavior by assuming that a proportion of the training labels are incorrect and belong with equality to the other classes. This could be done by randomly changing the labels at each training iterations. However, the same end can be achieved by changing the loss function to minimize the cross-entropy between the predicted distribution and a distribution where the true label has probability , and the other classes have equal probability. This is known as label smoothing and improves generalization in diverse scenarios.