Adam

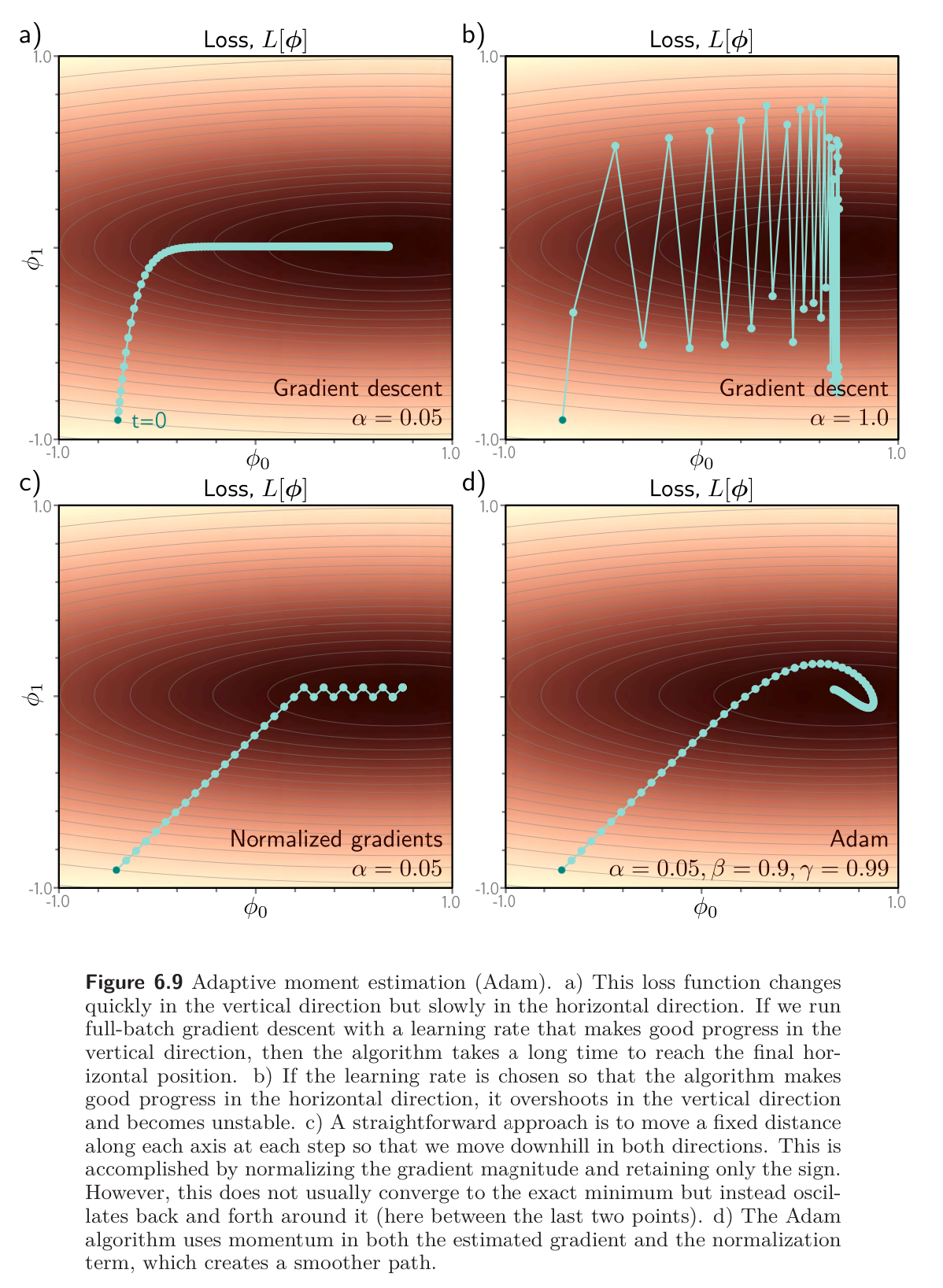
A big weakness of gradient descent with a fixed step size is that it makes large adjustments to parameters associated with large gradients (where perhaps we should be more cautious) and small adjustments to parameters associated with small gradients (where perhaps we should explore further). When the gradient of the loss surface is much steeper in one direction than another, it’s difficult to choose a learning rate that makes good progress in both directions and is stable.

Normalized gradients

A straightforward approach is to normalize the gradients so that we move a fixed distance (governed by the learning rate) in each direction.

To do this, we first measure the gradient ${\mathbf{m}}_{t+1}$ and the pointwise squared gradient ${\mathbf{v}}_{t+1}$:

$$\begin{array}{r}{\mathbf{m}}_{t+1}⟵\frac{\partial L[{\varphi }_t]}{\partial \varphi }\\ {\mathbf{v}}_{t+1}⟵{\left(\frac{\partial L[{\varphi }_t]}{\partial \varphi }\right)}^2\end{array}$$

Then we apply the update rule:

$${\varphi }_{t+1}⟵{\varphi }_t-\alpha \cdot \frac{{\mathbf{m}}_{t+1}}{\sqrt{{\mathbf{v}}_{t+1}}+ϵ}$$

where:

• The square root and division are both pointwise
• $\alpha$ is the learning rate
• $ϵ$ is a small constant that prevents division by zero

Essentially: the term ${\mathbf{v}}_{t+1}$ is the squared gradient, and its positive root is used to normalize the gradient itself, so all that remains is the sign in each coordinate direction. The result is that the algorithm moves a fixed distance $\alpha$ along each coordinate, where the direction is determined by whichever way is downhill.

This simple adjustment makes good progress in both directions but will not converge until it happens to land exactly at the minimum, instead, it will bounce around the minimum.

Adam

Adaptive moment estimation, or Adam, takes the idea of normalized gradients and adds momentum to both the estimate of the gradient and the squared gradient:

$$\begin{array}{rl}{\mathbf{m}}_{t+1}& ⟵\beta \cdot {\mathbf{m}}_t+(1-\beta )\frac{\partial L[{\varphi }_t]}{\partial \varphi }\\ {\mathbf{v}}_{t+1}& ⟵\gamma \cdot {\mathbf{v}}_t+(1-\gamma ){\left(\frac{\partial L[{\varphi }_t]}{\partial \varphi }\right)}^2\end{array}$$

where $\beta$ and $\gamma$ are the momentum coefficients for the two statistics.

Initialization bias correction: Using momentum is equivalent to taking weighted average over the history of each of these statistics. At the start of the procedure, all the previous measurements are effectively zero as we start with ${\mathbf{m}}_0=0,{\mathbf{v}}_0=0$, resulting in unrealistically small estimates. Consequently, we modify these statistics using the rule:

$$\begin{array}{r}{\tilde{\mathbf{m}}}_{t+1}⟵\frac{{\mathbf{m}}_{\mathbf{t}+1}}{1-{\beta }^{t+1}}\\ {\tilde{\mathbf{v}}}_{t+1}⟵\frac{{\mathbf{v}}_{t+1}}{1-{\gamma }^{t+1}}\end{array}$$

Since $\beta$ and $\gamma$ are in the range $[0,1)$, the terms with exponents $t+1$ become smaller with each time step, the denominators become closer to one, and this modification has a diminishing effect.

• Imagine trying to compute an average from just a few data points – we’d expect some bias just because we don’t have enough samples yet. This bias correction acts like a “smart guess” of what the average would have been with a longer history.

Finally, we update the parameters as before, but with modified terms:

$${\varphi }_{t+1}⟵{\varphi }_t-\alpha \cdot \frac{{\tilde{m}}_{t+1}}{\sqrt{{\tilde{\mathbf{v}}}_{t+1}}+ϵ}$$

The result is an algorithm that can converge to the overall minimum and makes good progress in every direction in the parameter space.

Note that Adam is usually used in a stochastic setting where the gradients and their squares are computed from mini-batches:

$$\begin{array}{rl}{\mathbf{m}}_{t+1}& ⟵\beta \cdot {\mathbf{m}}_t+(1-\beta )\sum _{i\in {\mathcal{B}}_t}\frac{\partial L[{\varphi }_t]}{\partial \varphi }\\ {\mathbf{v}}_{t+1}& ⟵\gamma \cdot {\mathbf{v}}_t+(1-\gamma ){\left(\sum _{i\in {\mathcal{B}}_t}\frac{\partial L[{\varphi }_t]}{\partial \varphi }\right)}^2\end{array}$$

so the trajectory is noisy in practice.

The gradient of neural network parameters can depend on their depth in the network; Adam helps compensate for this tendency and balances out changes across the different layers. In practice, Adam also has the advantage of being less sensitive to the initial learning rate because it avoids situations like those in figure 6.9 a-b (above), so it doesn’t need complex learning rate schedules.

Notes

Adam has become the default method for managing step sizes in neural networks. It combines the ideas of Momentum (ML) and adadelta.

• Take the average of the gradient
• Moderate step size based on magnitude of gradient

We start by writing the moving averages of the gradient and squared gradient, which reflect estimates of the mean and variance of the gradient for weight $j$:

$$\begin{array}{rl}{g}_{t,j}& ={\nabla }_{W}J(W_{t-1}{)}_j\\ m_{t,j}& =B_1{m}_{t-1,j}+(1-B_1)g_{t,j}\\ v_{t,j}& =B_2{v}_{t-1,j}+(1-B_2)g_{t,j}^2\end{array}$$

A problem with these estimates is that, if we initialize $m_0=v_0=0$, they will always be biased (slightly too small). So we will correct for that bias by defining:

$$\begin{array}{rl}{\hat{m}}_{t,j}& =\frac{m_{t,j}}{1-B_1^t}\\ {\hat{v}}_{t,j}& =\frac{v_{t,j}}{1-B_2^t}\\ W_{t,j}& =W_{t-1,j}-\frac{\eta }{\sqrt{{\hat{v}}_{t,j}+ϵ}}{\hat{m}}_{t,j}\end{array}$$

Note that $B_1^t$ is $B_1$ raised to the power of $t$ and likewise for $B_2^t$. To justify these corrections, note that if we were to expand $m_{t,j}$ in terms of $m_{0,j}$ and $g_{0,j},g_{1,j},\dots ,g_{t,j}$ the coefficients would sum to $1.$ However, the coefficient behind $m_{0,j}$ is $B_1^t$ and since $m_{0,j}=0$, the sum of coefficients of non-zero terms is $1-B_1^t$ , hence the correction. The same justification holds for $v_{t,j}$.

Now, our update for weight $j$ has a step size that takes the steepness into account (like Adadelta) but also tends to move in the same direction (like momentum). The authors of adam like setting:

• $B_1=0.9$
• $B_2=0.990$
• $ϵ=10^{-8}$

Although we now have even more parameters, adam is not highly sensitive to their values. Even though we now have a step-size for each weight, and we have to update various quantities on each iteration of gradient descent, it’s relatively easy to implement by maintaining a matrix for each quantity $(m_t^l,v_t^l,g_t^l,g_t^{2^l})$ in each layer of the network.