Uniform-cost search is a graph search algorithm used in artificial intelligence and computer science to find the lowest-cost path from a start node to a goal node.
It always expands the node that can be reached with the smallest total path cost so far, rather than the fewest steps. This makes it suitable for problems where actions have different costs.
The algorithm works by keeping a priority queue (often called the frontier) ordered by cumulative cost. It begins with the start node at cost zero. At each step, it removes the node with the lowest accumulated cost, checks whether it is a goal, and if not, expands it by adding its successors to the queue with their updated costs. If a cheaper path to an already-seen node is found, the algorithm updates it.
Uniform-cost search is complete (it will find a solution if one exists) and optimal (it guarantees the least-cost solution), provided all step costs are non-negative.
Conceptually, it is a generalization of breadth-first search. Breadth-first search can be seen as a special case of uniform-cost search where every step has the same cost. It is also closely related to Dijkstra’s Algorithm; in fact, uniform-cost search is essentially Dijkstra’s algorithm used for goal-directed search.
Its main drawback is efficiency: because it explores all cheaper paths before more expensive ones, it can consume significant time and memory in large or complex search spaces.
Example:
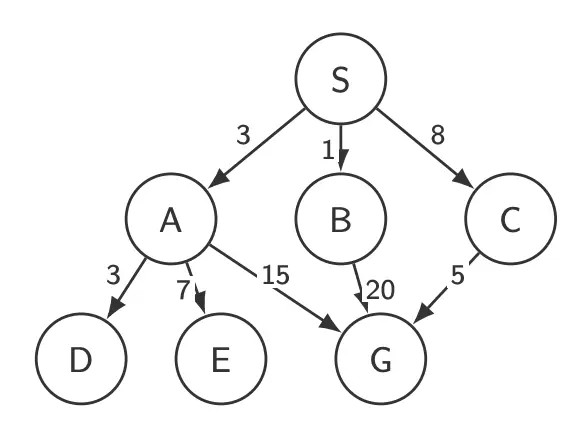
- Expanded path: S, B, A, D, C, E, G
- Returned solution: S, C, G (cost=13)