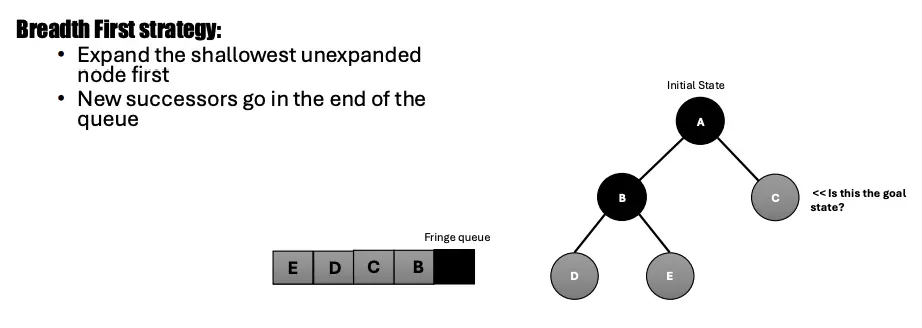
In BFS, we traverse a search tree by expanding the shallowest unexpanded node first. The fringes are added in a FIFO queue, which guarantees level-by-level exploration. Thus, we explore the state space in waves of increasing depth.
Algorithm

Properties
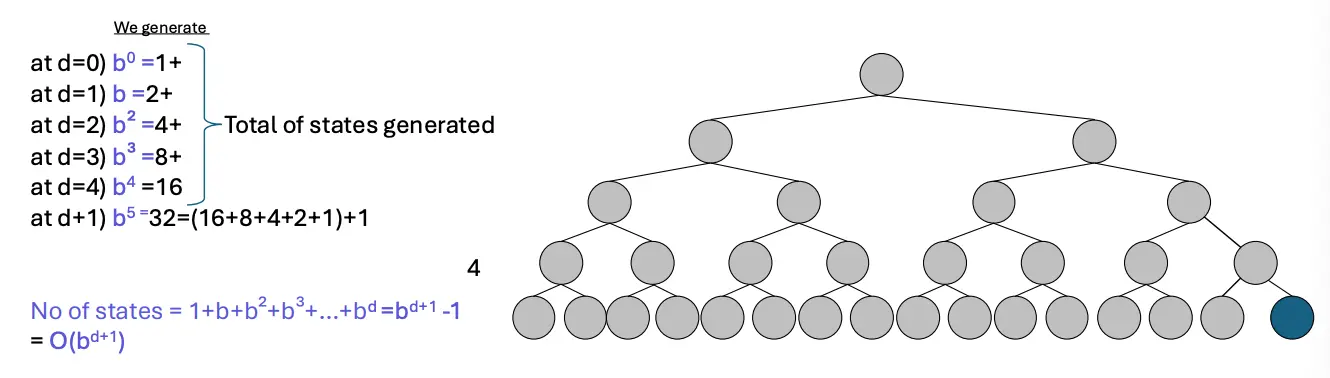
Number of states and upper bound
The upper bound case of BFS is where the goal is the last node of depth .
Time and space complexity
From the above, we can see that both the time and space complexity are given by
where
- is the branching factor (maximum number of children at each node)
- is the depth of the solution
This cost is quite high. For example, with depth = 14, we would have nodes, which would take ~3000 years and 1 exabyte.
Completeness and optimality
BFS is:
- Complete, if is finite
- Optimal, if path cost is equal to depth (all operators have the same cost). It is guaranteed to return the shallowest goal (depth ).
If step costs vary, BFS may return a non-optimal solution. It would ignore cheaper but deeper paths. We can think of BFS as optimizing the number of steps, not the cost, energy, or delay.
Examples
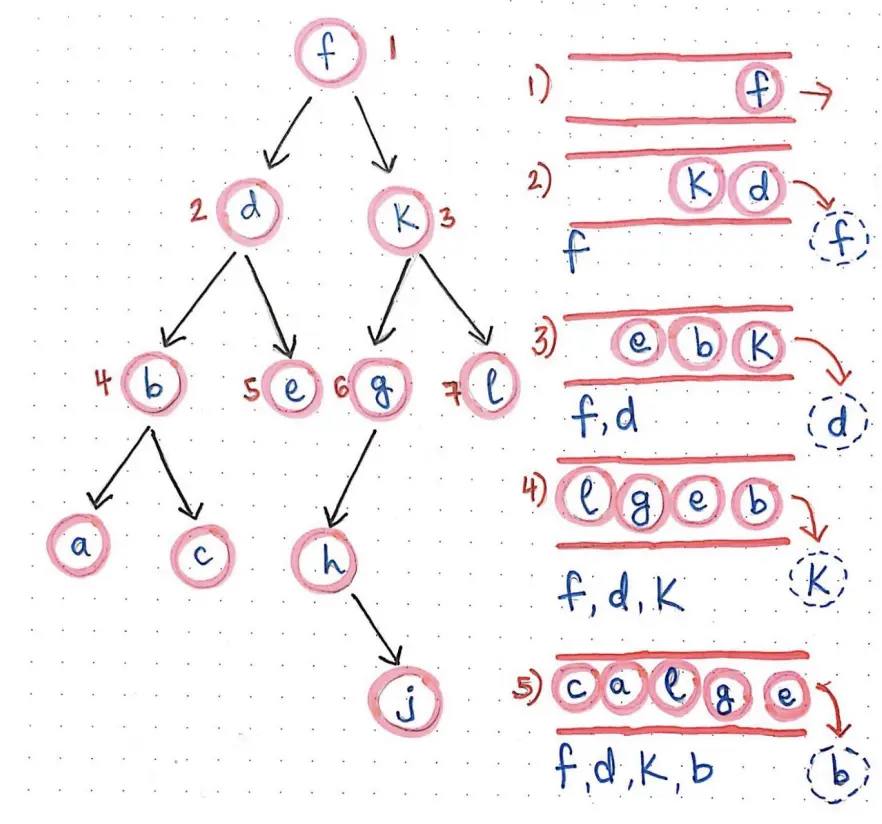
- Problem: Search for state
We search through a tree one level at a time. We traverse through one entire level of children nodes first, before moving on to traverse through the grandchildren nodes. Similarly, we traverse through on entire level of grandchildren nodes before going on to traverse great-grandchildren nodes.

First, we expand the shallowest unexpanded node. New successors go in the end of the queue. (Right side is the start of queue for some reason)

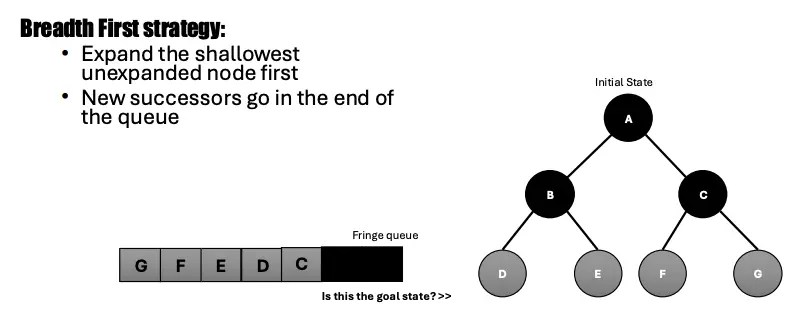
Another example: