Numerical Integration for Control Systems

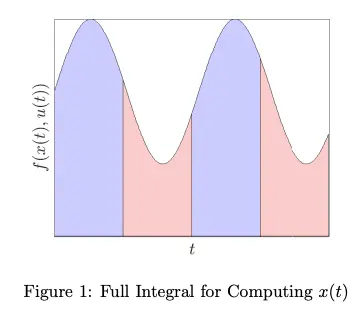
Starting with a system in continuous time:

$$\begin{array}{r}\dot{x}=f(x,u)\\ y=g(x,u)\end{array}$$

In LTI systems, we could write an explicit solution for a given $t$; however, we cannot do this for the vast majority of non-linear systems.

Thus, we aim to simulate the system:

• Goal: Determine the trajectory $x(t)$ for the system for some initial condition
• Challenge: Computers operate in discrete time

To solve, this we approximate continuous-time system with a related discrete time system.

First, we fix $T>0$ and assume $t=nT$ for some positive integer $n$.

$$\begin{array}{rl}x(t)& ={\int }_0^{t}f(x(s),u(s))ds\\ & ={\int }_0^{T}f(x(s),u(s))ds+{\int }_T^{2T}f(x(s),u(s))dx+\cdots +{\int }_{(n-1)T}^{nT}f(x(s),u(s))ds\\ & =\sum _{k=0}^{n-1}\underset{=:\Delta [k+1]}{\underbrace{{\int }_{kT}^{(k+1)T}f(x(s),u(s))}}ds\\ & =\sum _{k=0}^{n-1}\Delta [k+1]\end{array}$$

This procedure involves summing the area under the curve in the figure below:

Say we know the value of $x$ at time $t=nT$, then

$$x((k+1)T)=x(kT)+\Delta [k+1]$$

This is still exact because $\Delta [k+1]$ is defined with the integral of a continuous-time function, but this is intractable to solve.

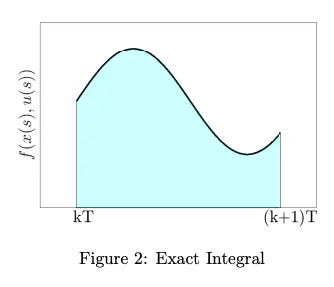
Thus, the idea is then to approximate $\Delta [k+1]$ using a finite number of discrete points.

Left-side rule - Euler Integration

$$\Delta [k+1]\approx {\int }_{kT}^{(k+1)T}f(x(kT),u(kT))ds=Tf(x(kT),u(kT))$$

This is essentially Euler integration.

Right side rule - Backwards Euler integration

$$\Delta [k+1]\approx {\int }_{kT}^{(k+1)T}f(x(kT),u(kT))ds=Tf(x(k+1)T,u(k+1)T)$$

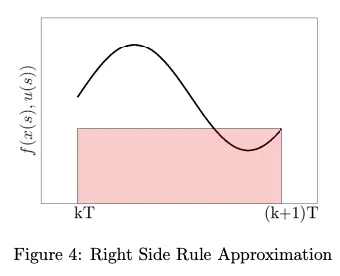
This is backward Euler integration.

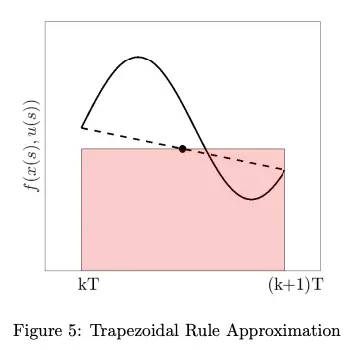
Trapezoid Rule

$$\Delta [k+1]=\frac{T}{2}[f(x(kT),u(kT))+f(x((k+1)T),u((k+1)T))]$$