Involute Gear Tooth

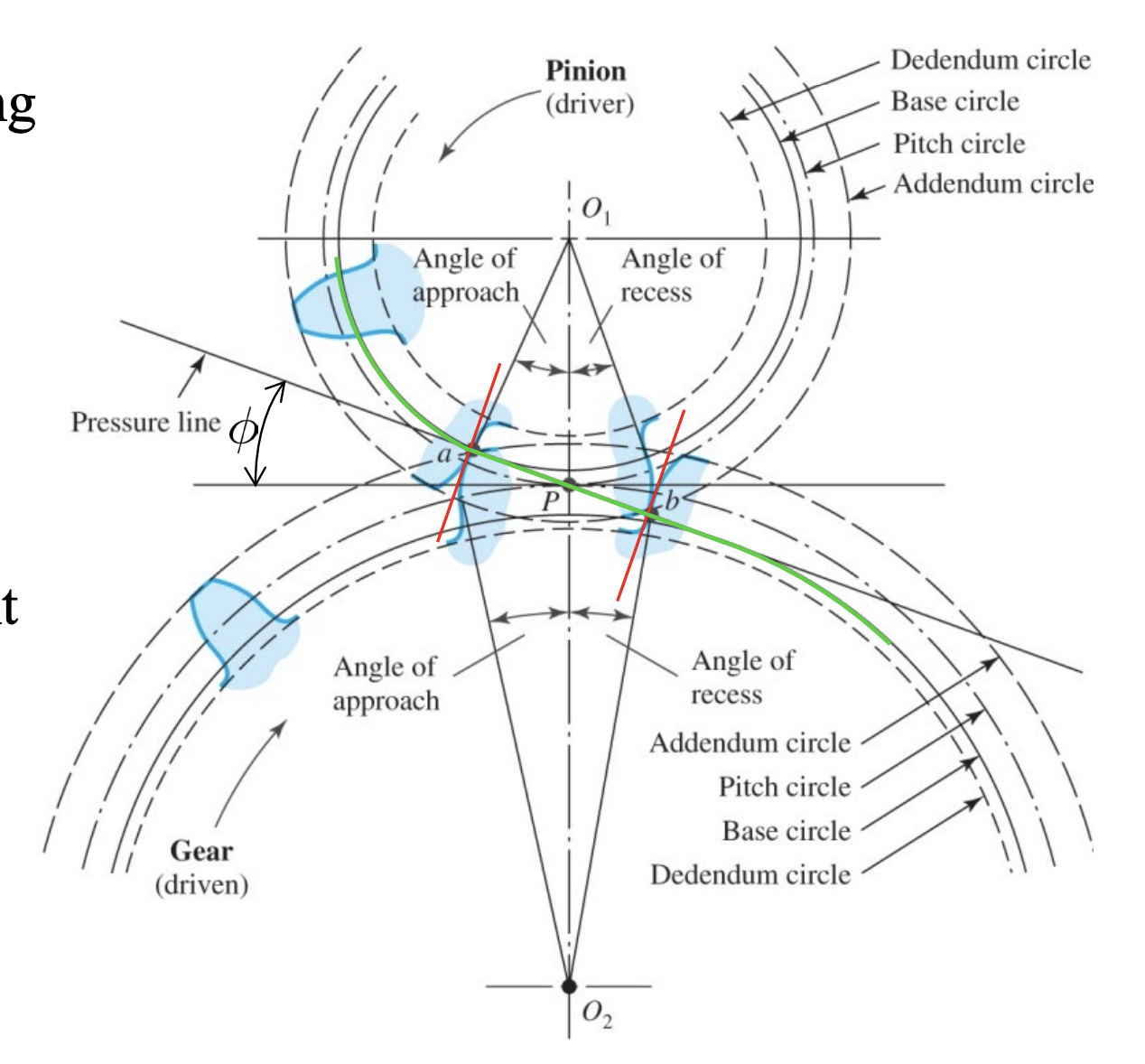
The involute tooth form is one of the standard gear shapes.

The involute curve is generated by unwrapping a taut string from a cylinder:

• Animated explainer: Involute Gears Explained

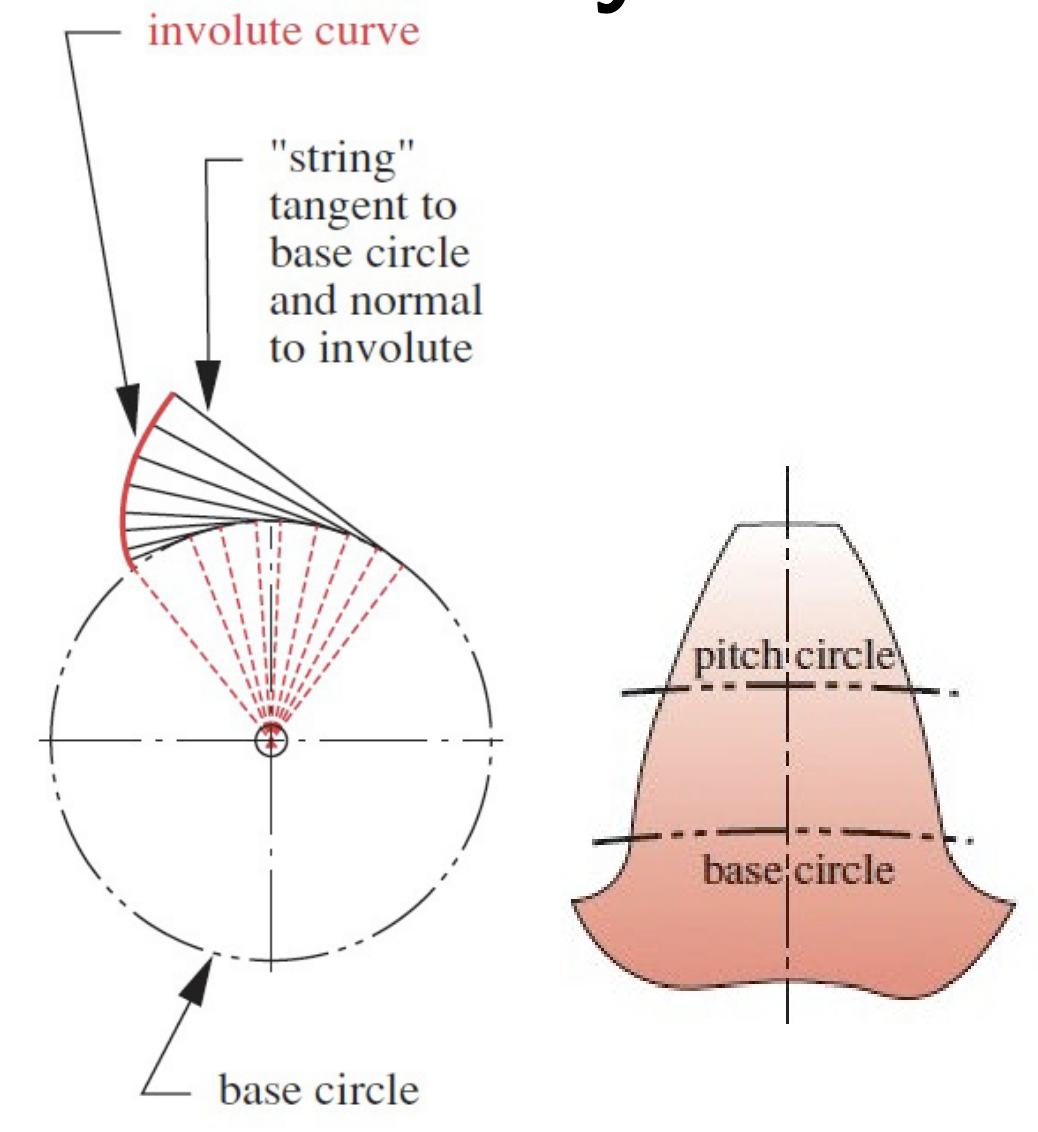
• The string is always tangent to the base circle
• The center of curvature of the involute is always at the point of tangency of the string with the base circle
• A tangent to the involute is always normal to the string which is the instantaneous radius of curvature of the involute curve

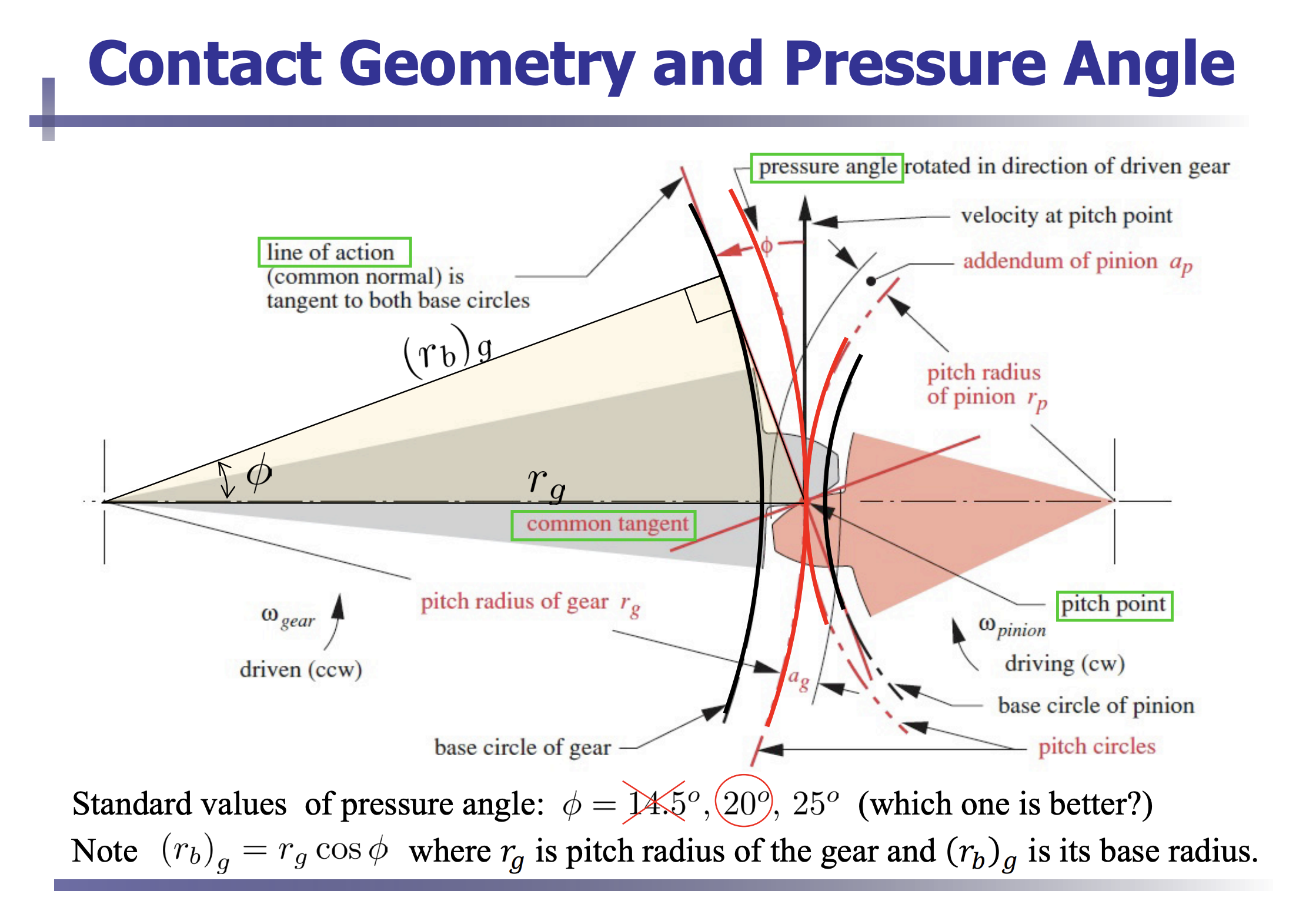
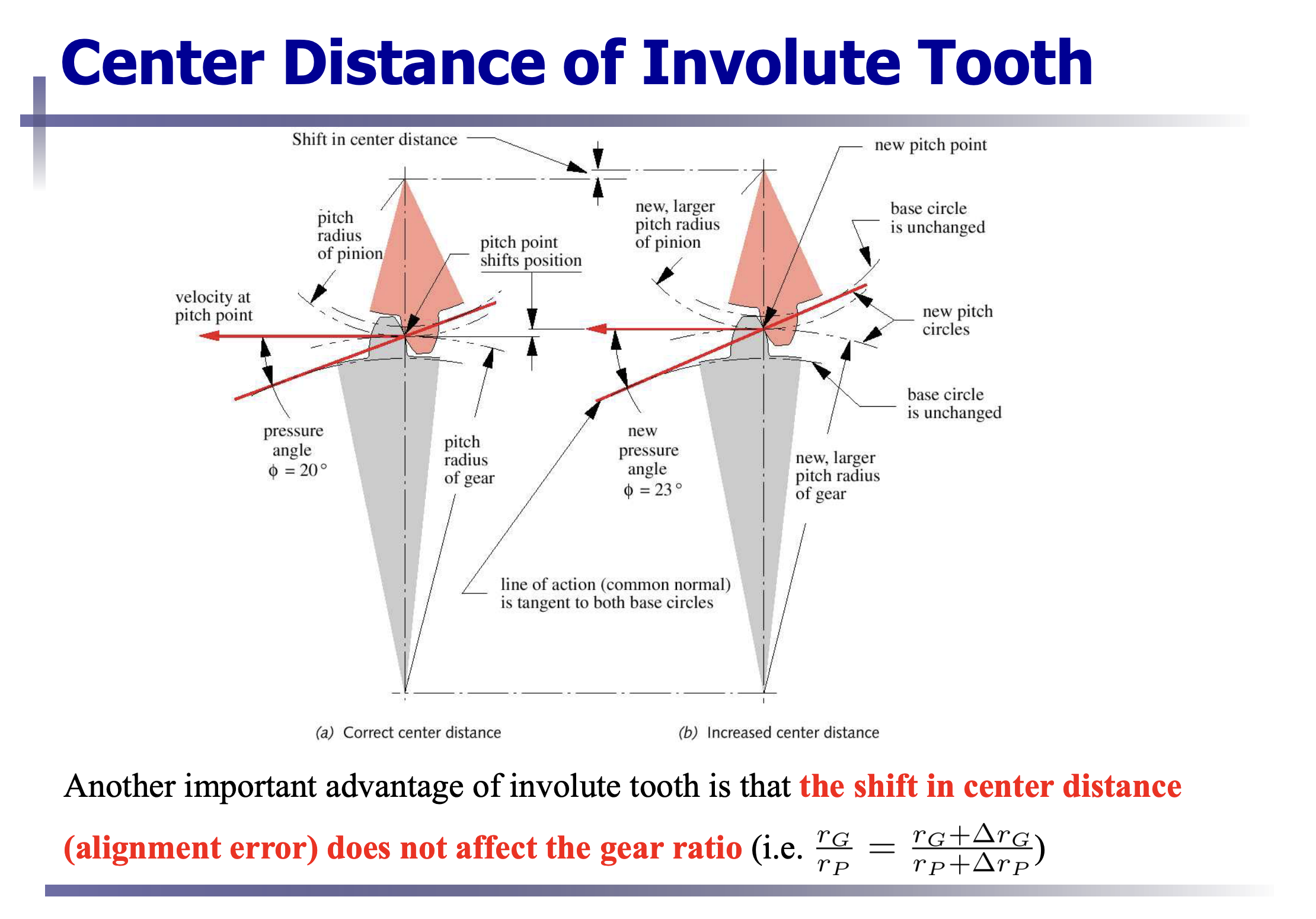
Involute Shape for Law of Gearing

• The point of contact moves along the line $ab$ during meshing as if two pitch circles are rotating in different directions to keep the string tight.
• Therefore, when the pinion is rotating at a constant speed, the gear is also rotating at a constant speed, hence the speed ratio remains constant during meshing.