Fluid Element Kinematics

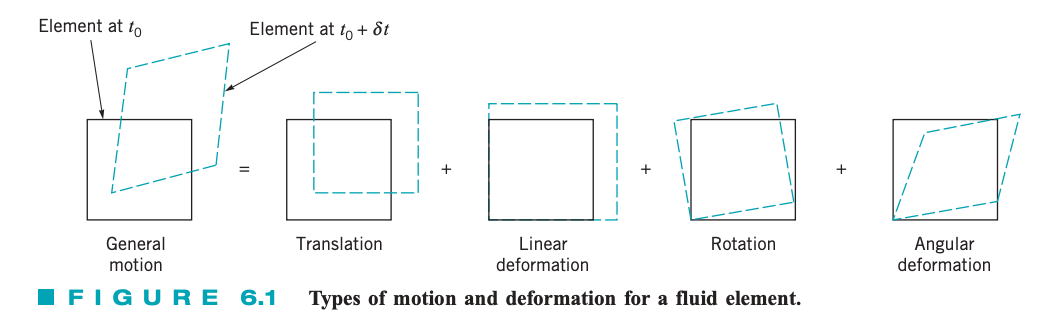
We want to form a mathematic description of the motion of fluid elements moving in a flow field. A small fluid element in the shape of a cube which is initially in one position will move to another position during a short time interval $\delta t$. We expect the element not only to translate but also have its volume changed (linear deformation), rotate, and undergo change in shape (angular deformation).

Recall that the velocity field can be described by specifying the velocity $\mathbf{V}$ at all points, and we can write velocity as

$$\mathbf{V}=u\mathbf{i}+v\mathbf{j}+w\mathbf{k}$$

and the acceleration can be written as

$$\mathbf{a}=\frac{D\mathbf{V}}{Dt}=\frac{\partial \mathbf{V}}{\partial t}+u\frac{\partial \mathbf{V}}{\partial x}+v\frac{\partial \mathbf{V}}{\partial y}+w\frac{\partial \mathbf{V}}{\partial z}$$

Linear Motion and Deformation

Consider a small fluid cube is considered at time $t$ and then at $t+dt$. Velocity $u(x)$ varies with $x$, so different points in the fluid move differently. The element stretches as a result.

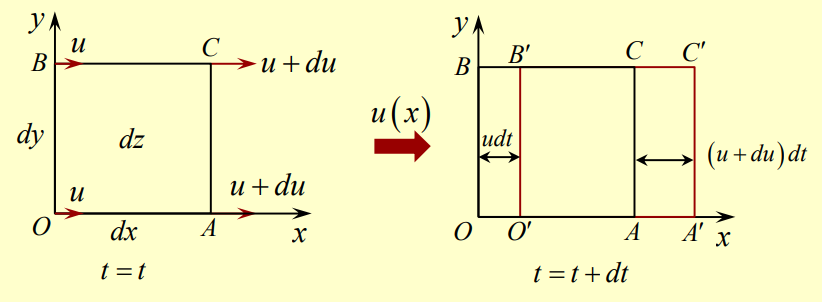
• Initially, side $OA=dx,OB=dy$.
• The change in velocity is given by $du=\frac{\partial u}{\partial x}dx$
• After some time $dt$, point $O$ moves to $O^{\prime }$ by $udt$, and point $A$ moves to $A^{\prime }$ by an amount $(u+du)dt$

Then, the linear deformation is given as

$$\begin{array}{rl}{O}^{\prime }{A}^{\prime }& =O^{\prime }A+A{A}^{\prime }\\ & =dx-udt+(u+du)dt\\ & =dx+dudt\end{array}$$

The initial volume was

$$\delta V=dx\cdot dy\cdot dz$$

Final volume:

$$\delta V^{\prime }=(dx+dudt)\cdot dy\cdot dz$$

The change in volume is given by

$$\delta V^{\prime }-\delta V=dudydzdt$$

Since we have $du=\frac{\partial u}{\partial x}dx$, we can write the above as

$$\delta V^{\prime }-\delta V=\frac{\partial u}{\partial x}dxdydzdt$$

The rate of volume change can then be written as

$$\frac{d(\delta V)}{dt}=\frac{\partial u}{\partial x}dx\cdot dy\cdot dz$$

The rate per unit volume in the $x,y,z$ directions is given as

$$\begin{array}{r}\frac{1}{\delta V}\frac{d(\delta V)}{dt}=\frac{\partial u}{\partial x}\\ \frac{1}{\delta V}\frac{d(\delta V)}{dt}=\frac{\partial v}{\partial y}\\ \frac{1}{\delta V}\frac{d(\delta V)}{dt}=\frac{\partial w}{\partial z}\end{array}$$

Combining the above, the volume change rate per unit volume

$$\frac{1}{\delta V}\frac{d\delta V}{dt}=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=\nabla \cdot \mathbf{V}$$

This is called the volumetric dilatation rate.

Angular Motion and Deformation

Now consider a fluid element experiencing velocity gradients in both $u(y)$ and $v(x)$.

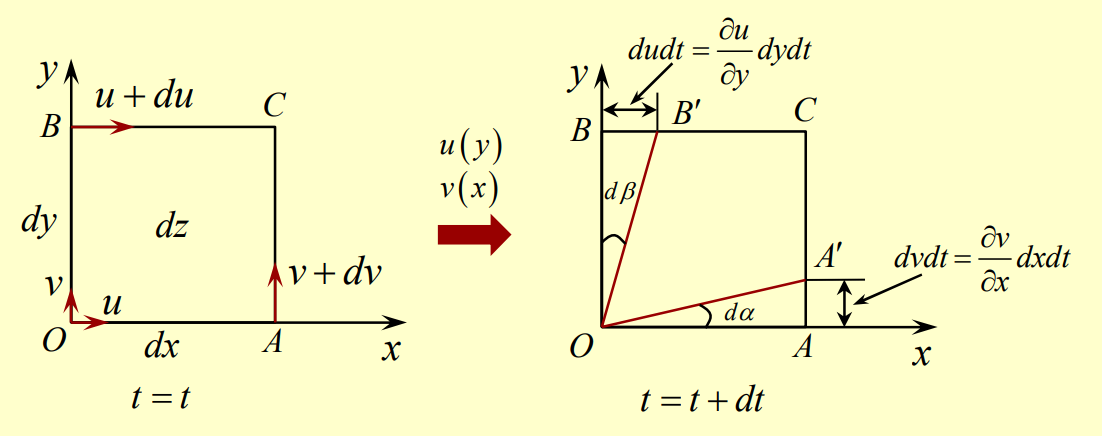
The angle at corner $O$ changes over time:

• ${\omega }_{OA}=\frac{d\alpha }{dt}$ (due to motion along side $OA$)
• ${\omega }_{OB}=\frac{d\beta }{dt}$ (due to motion along side $OB$) where we can say that

$$d\alpha \approx \tan (d\alpha )=\frac{\frac{\partial v}{\partial x}dx\cdot dt}{dx}=\frac{\partial v}{\partial x}dt$$

Similarly, $d\beta \approx \frac{\partial u}{\partial y}$.

We use the right hand rule to define counterclockwise as positive:

$$\begin{array}{r}{\omega }_{OA}>0\text{ if }\frac{\partial v}{\partial x}>0\\ {\omega }_{OB}<0\text{ if }\frac{\partial u}{\partial y}>0\end{array}$$

The net angular velocity in the $z$-direction, ${\omega }_z$, of the element is found by taking the average rotation rate of the two sides:

$${\omega }_z=\frac{1}{2}\left(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right)$$

This can be generalized to the other directions as well:

$$\begin{array}{r}{\omega }_x=\frac{1}{2}\left(\frac{\partial w}{\partial y}-\frac{\partial v}{\partial z}\right)\\ {\omega }_y=\frac{1}{2}\left(\frac{\partial u}{\partial z}-\frac{\partial w}{\partial x}\right)\end{array}$$

and we can say that the overall angular velocity vector is

$$\omega ={\omega }_x\mathbf{i}+{\omega }_y\mathbf{j}+{\omega }_z\mathbf{k}$$

Vorticity

Vorticity is the curl of the velocity vector:

$$\begin{array}{rl}\zeta =\nabla \times \mathbf{V}& =\left|\begin{array}{ccc}\mathbf{i}& \mathbf{j}& \mathbf{k}\\ \frac{\partial }{\partial x}& \frac{\partial }{\partial y}& \frac{\partial }{\partial z}\\ u& v& w\end{array}\right|\\ & =\left(\frac{\partial w}{\partial y}-\frac{\partial u}{\partial z}\right)\mathbf{i}+\left(\frac{\partial u}{\partial z}-\frac{\partial w}{\partial z}\right)\mathbf{j}+\left(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right)\mathbf{k}\end{array}$$

Note that angular velocity is just half of vorticity:

$$\omega =\frac{1}{2}\zeta =\frac{1}{2}\nabla \times \mathbf{V}$$

If $\zeta =0$, then $\omega =0$, which means that ${\omega }_x={\omega }_y={\omega }_z=0$, resulting in an irrotational flow.

Shearing Strain and Strain Rate

The shearing strain is given by

$$\delta \gamma =d\alpha +d\beta$$

The rate of shearing strain is given by

$$\dot{\gamma }=\underset{\delta t\to 0}{\lim }\frac{\delta \gamma }{\delta t}={\omega }_{OA}+{\omega }_{OB}=\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}$$

which measures how fast the fluid elements is distorting (shearing), not rotating.