Energy Equations for Fluid Flow

Uniform Flows

In a uniform flow, kinetic energy is consistent across sections. The standard Bernoulli Equation applies:

$$\frac{p_1}{\gamma }+\frac{V_1^2}{2g}+z_1=\frac{p_2}{\gamma }+\frac{V_2^2}{2g}+z_2+h_L$$

where $h_L$ is head loss due to friction and turbulence.

Non-Uniform Flows

For non-uniform velocity distributions, the kinetic energy coefficient ($\alpha$) is introduced:

$$\frac{p_1}{\gamma }+{\alpha }_1\frac{V_1^2}{2g}+z_1=\frac{p_2}{\gamma }+{\alpha }_2\frac{V_2^2}{2g}+z_2+h_L$$

The coefficient is determined by:

$$\int \frac{V^2}{2}\rho \mathbf{V}\cdot \mathbf{n}dA=\dot{m}\left(\frac{{\alpha }_{\text{out}}{\overline{V}}_{\text{out}}^2}{2}-\frac{{\alpha }_{\text{in}}{\overline{V}}_{\text{in}}^2}{2}\right)$$

• $\alpha =1$ – Uniform $\mathbf{V}$
• $\alpha >1$ – Non-uniform $\mathbf{V}$

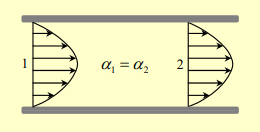
Note that $\alpha$ is determined by the velocity profile. For example, in fully developed laminar flow, $\alpha >1$, since the velocity profile is parabolic. In fully developed turbulent flow, it would be closer to $1$ because of a flatter velocity profile.

Head Loss

The standard energy balance including head loss is

$$\frac{p_1}{\gamma }+z_1=\frac{p_2}{\gamma }+z_2+h_L$$

representing the drop in hydraulic head due to friction and other factors along the pipe.

Frictional head loss can be written as

### Inclined Pipe For a pipe inclined at an angle $\theta$, the gravitational component along the pipe axis influences the head loss. The energy equation becomes: $$ \begin{align} \frac{\Delta p}{\gamma} +(z_{1}-z_{2}) & = h_{L} \\[2ex] \Delta p - \gamma (z_2 - z_1) & = \gamma h_L \\[2ex] \Delta p - \gamma l \sin \theta & =\gamma h_{L} \end{align} $$ We can then write $$ \frac{\Delta p - \gamma l\sin \theta}{l} = \frac{\gamma h_{L}}{l}=\frac{2\tau}{r} $$ where $h_{L}$ is head loss due to friction. This also applies to horizontal flow as we can just use $\theta=0$. This in turn leads to: $$ h_L = \frac{2 \tau_w \ell}{\gamma r} = \frac{4 \tau_w \ell}{\gamma D} $$