Differential Fluid Elements Forces and Equations of Motion

Fluid Conservation of Momentum is fundamentally linked to understanding the forces acting on differential fluid elements. There are two types of forces we need to consider: body forces and surface forces.

Body Forces

Body force act throughout the volume of the fluid element. The main one is gravitational force – the weight of the fluid element due to gravity, given by

$$\delta {\mathbf{F}}_B=\delta m\cdot g$$

where $\delta m=\rho dV$ is the mass of the element and $g$ is the gravitational acceleration.

Other examples include magnetic and electrostatic forces.

Surface Forces

Surface forces act on the surface of the fluid element. They are distributed over differential surface areas and include:

• Normal stresses $\sigma$ – Forces perpendicular to the surface
• Shearing stresses $\tau$ – Forces parallel to the surface

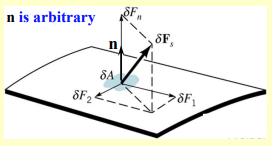
In the above diagram we see a surface force with a normal component $\delta F_n$ and shear force components $\delta F_1$ and $\delta F_2$.

As the differential area $\delta A$ approaches zero, the force per unit area defines the stresses.

Normal stress:

$${\sigma }_n=\underset{\delta A\to 0}{\lim }\frac{\delta F_n}{\delta A}$$

• Intensity of the normal force distributed over the surface area; perpendicular to the surface.

Shear stresses:

$${\tau }_1=\underset{\delta A\to 0}{\lim }\frac{\delta F_1}{\delta A},{\tau }_2=\underset{\delta A\to 0}{\lim }\frac{\delta F_2}{\delta A}$$

• Intensity of the parallel tangential forces; act to distort or shear the fluid element

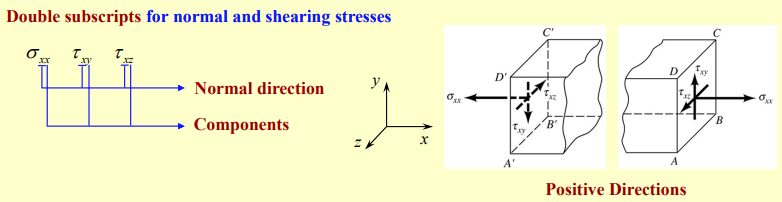
We use double subscripts to specify the plane on which the stress acts and the direction of the stress. For example:

• ${\sigma }_{xx}$ → Normal stress on the x-plane in the x-direction.
• ${\tau }_{xy}$ → Shear stress on the x-plane in the y-direction.

Equations of Motion

We can use the forces derived above to derive the equations of motion through control volume analysis. We consider a differential fluid element cube with dimensions $dx,dy,dz$.

First, we start with the surface forces in the $x$ direction.

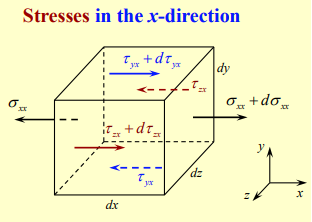
In total, we have:

$$\begin{array}{rl}\delta F_{S,x}& =({\sigma }_{xx}+d{\sigma }_{xx})dydz-{\sigma }_{xx}dydz\\ & +({\tau }_{yx}+d{\tau }_{yx})dxdz-{\tau }_{yx}dxdz+({\tau }_{zx}+d{\tau }_{zx})dxdy-{\tau }_{zx}dxdy\\ & =d{\sigma }_{xx}dydz+d{\tau }_{yx}dxdz+d{\tau }_{zx}dxdy\end{array}$$

We can consider the Taylor expansions for these components. For example,

$$d{\sigma }_{xx}=\frac{\partial {\sigma }_{xx}}{\partial x}dx+\text{cancelto}0\frac{\partial {\sigma }_{xx}}{\partial y}dy+\text{cancelto}0\frac{\partial {\sigma }_{xx}}{\partial z}dz$$

Similarly, we have

$$\begin{array}{r}d{\tau }_{yx}=\frac{\partial {\tau }_{yx}}{\partial y}dy\\ d{\tau }_{zx}=\frac{\partial {\tau }_{zx}}{\partial z}dz\end{array}$$

Thus, our previous expression for the total $x$ direction forces becomes

$$\delta F_{S,x}=\frac{\partial {\sigma }_{xx}}{\partial x}dxdydz+\frac{\partial {\tau }_{yx}}{\partial y}dxdydz+\frac{\partial {\tau }_{zx}}{\partial z}dxdydz$$

And similarly in the $y$ and $z$ directions we have

$$\begin{array}{rl}\delta F_{S,y}& =\left(\frac{\partial {\tau }_{xy}}{\partial x}+\frac{\partial {\sigma }_{yy}}{\partial y}+\frac{\partial {\tau }_{zy}}{\partial z}\right)dxdydz\\ \delta F_{S,z}& =\left(\frac{\partial {\tau }_{xz}}{\partial x}+\frac{\partial {\tau }_{yz}}{\partial y}+\frac{\partial {\sigma }_{zz}}{\partial z}\right)dxdydz\end{array}$$

In vector form we can combine all three to have:

$$\delta {\mathbf{F}}_s=\delta F_{S,x}\mathbf{i}+\delta F_{S,y}\mathbf{j}+\delta F_{S,z}\mathbf{k}$$

For body forces we have:

$$\delta {\mathbf{F}}_B=\delta m\cdot \mathbf{g}=\delta m\cdot g_x\mathbf{i}+\delta m\cdot g_y\mathbf{j}+\delta m\cdot g_z\mathbf{k}$$

And the total forces are:

$$\delta \mathbf{F}=\delta {\mathbf{F}}_S+\delta {\mathbf{F}}_B=\delta m\cdot \mathbf{a}=\rho dxdydz\cdot \mathbf{a}$$

Applying Newton’s second law in $x$ direction gives:

$$\begin{array}{rl}\delta F=\delta F_S+\delta F_B& =\rho dV\mathbf{a}\\ \frac{\partial {\sigma }_{xx}}{\partial x}dxdydz+\frac{\partial {\tau }_{yx}}{\partial y}dxdydz+\frac{\partial {\tau }_{zx}}{\partial z}dxdydz+\rho dxdydz\cdot g_x& =\rho dxdydz\cdot a_x\end{array}$$

This can be extended in all three directions to get equations of motion for each direction:

$$\boxed{\begin{array}{rl}x:& \frac{\partial {\sigma }_{xx}}{\partial x}+\frac{\partial {\tau }_{yx}}{\partial y}+\frac{\partial {\tau }_{zx}}{\partial z}+\rho g_x=\rho \left(\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}\right)\\ y:& \frac{\partial {\tau }_{xy}}{\partial x}+\frac{\partial {\sigma }_{yy}}{\partial y}+\frac{\partial {\tau }_{zy}}{\partial z}+\rho g_y=\rho \left(\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z}\right)\\ z:& \frac{\partial {\tau }_{xz}}{\partial x}+\frac{\partial {\tau }_{yz}}{\partial y}+\frac{\partial {\sigma }_{zz}}{\partial z}+\rho g_z=\rho \left(\frac{\partial w}{\partial t}+u\frac{\partial w}{\partial x}+v\frac{\partial w}{\partial y}+w\frac{\partial w}{\partial z}\right)\end{array}}$$