Coupon bonds pay regular coupon interest payments based on the coupon rate. Then they pay face value at maturity.
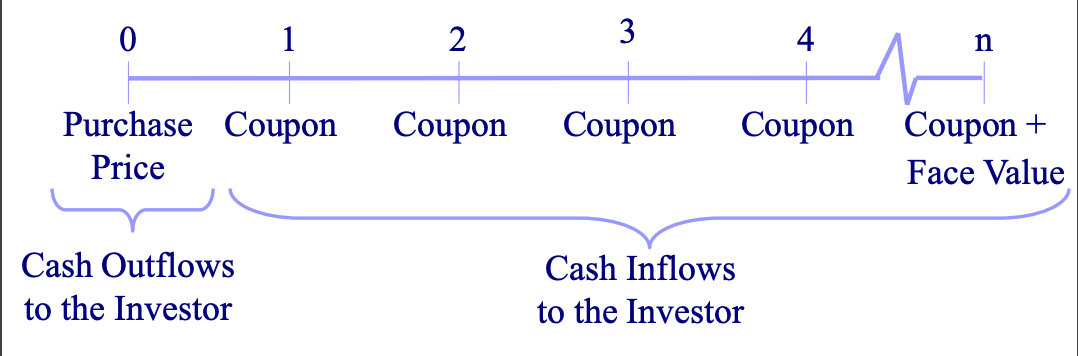
The coupons can be treated as an annuity.
When talking about bonds, we generally talk about yields. The price of the bond is the present value of future cash flows. Higher yield means higher discount rate, which means lower present value of future cash flows; thus, the price of the bond is lower, which is bad for bond investors. This is the opposite of the stock market.
Yield to Maturity of Coupon Bonds
Consider a five-year, 963.11, what is the bond’s yield to maturity?
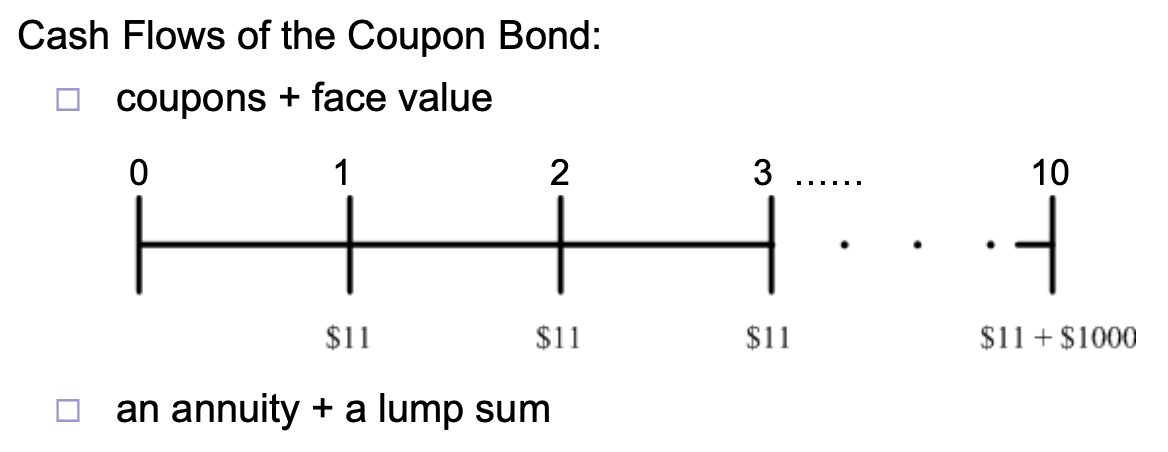
We consider the PV as outflow (negative), while the PMT and FV are inflows (positive). Since the payments are semiannual, we have .

This gives yield = 1.5%, but this is for a six-month period. We multiply by 2 to get APR. The yield to maturity is the discount rate that equates the present value of the bond’s cash flows with its price.
The yield to maturity is not a guaranteed rate of return; it’s a promised yield assuming:
- The investor buys the bond and holds until maturity
- Interim cash flows can be reinvested at YTM
- No default of coupon or maturity value
Computing Coupon Bond Price
Consider again the five-year $1000 bond with a 2.2% coupon rate and semiannual coupons. Suppose interest rates drop and investors now only demand a yield to maturity of 2% (expressed as an APR with semiannual compounding). What price will the bond be trading for?
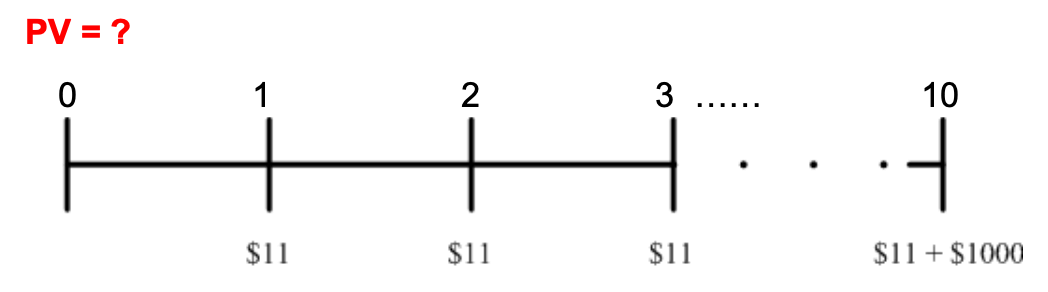
We have:

Given that investors have lowered the required rate of return from investing in it from 1.5% to 1% per 6-month period, the bond’s price will rise to $1009.47.
Market interest rates have dropped, the bond’s yield will fall so that it is in line with the lower competitive rates being offered for similar risk and maturity elsewhere in the market. Since the cash flows from investing in the bond remain the same, its PV will be higher at a lower discount rate.
In general, the price of a coupon bond is:
- First term is the PV of all periodic coupon payments (annuity)
- Second term is the PV of the face value repayment using the YTM
- Thus, the Purchase Price or Market Price of a bond is simply the present value of the cash inflows, discounted at the bond’s yield-to-maturity
Discount and Premium Bonds
Consider three 30-year bonds with annual coupon payments. One bond has a 10% coupon rate, one has a 5% coupon rate, and one has a 3% coupon rate. If the yield to maturity of each bond is 5%, what is the price of each bond per $100 face value? Which bond trades at a premium, which trades at a discount, and which trades at par?

- Premium/Above par: Bond price > Face Value, or Coupon rate > YTM
- At par: Bond value = Face Value, or Coupon Rate = YTM
- Discount/Below par: Bond price < Face Value, or Coupon Rate < YTM
The terms “discount” and “premium” are simply descriptive and are not meant to imply that you should try to buy bonds at a discount and avoid buying bonds at a premium. In a competitive market, the Law of One Price ensures that all similar bonds are priced to earn the same return. When you buy a bond, the price exactly equals the present value of the bond’s cash flows, so that you earn a fair return, but not an abnormally good (or bad) return.