Bond Pricing

Bond prices are inversely related to interest rates:

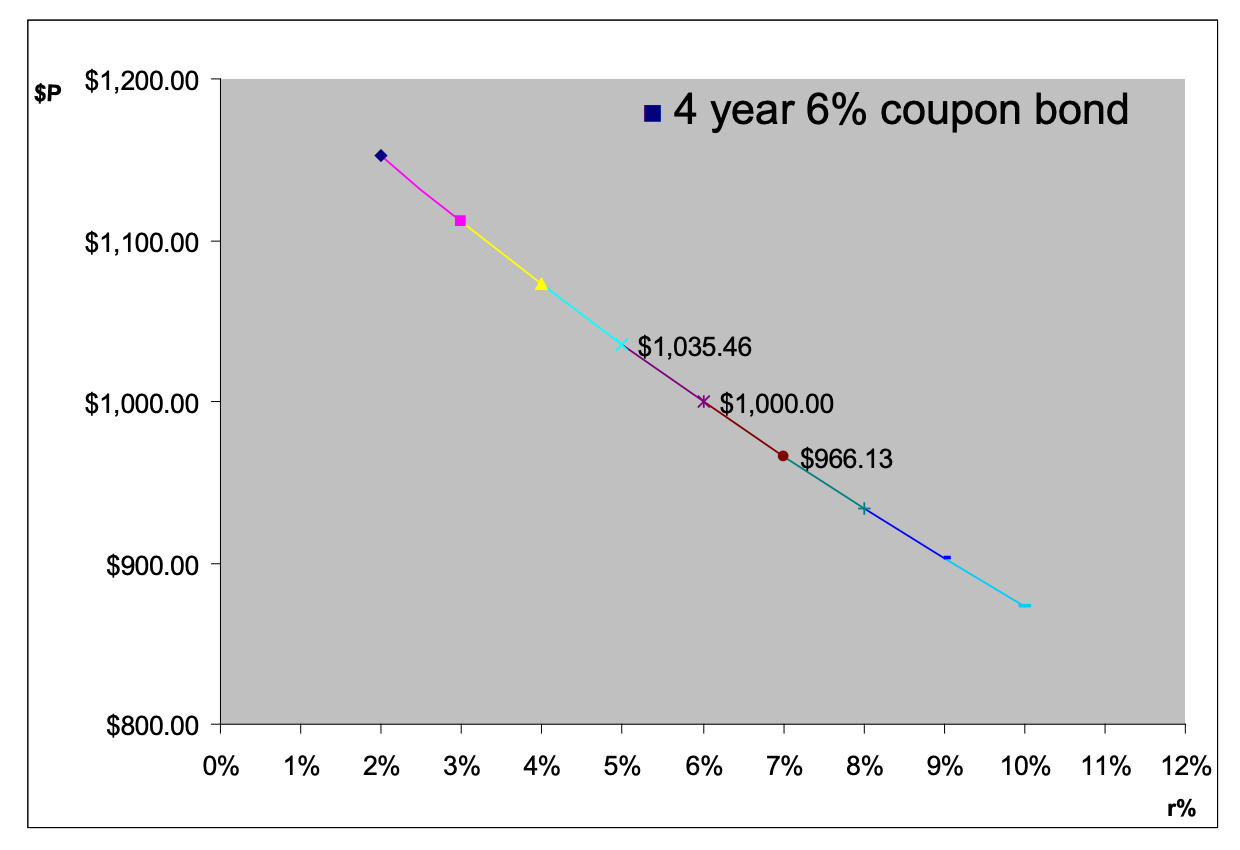
Essentially, the incomes (coupons and face value at maturity) are fixed – hence they’re called fixed income securities. Thus, for yield to maturity of a bond to match the prevailing market interest, its price must change. To get higher YTM to match higher interest rates, we need price to fall. To get lower YTM to match lower interest rates, we need price to rise.

Basic Bond Pricing Example

Suppose we have bond that pays $50couponperyear(from5$1000 bond).

Case 1 – Market interest rates rise to 6%:

• New bonds are being issued that pay $60/year
• Our bond only pays $50, which is less attractive to buyers
• Thus, to sell it, we would need to drop the price so that our bond’s total return (coupon + face value at maturity) matches the 6% interest rate
• Price falls → YTM rises to match market rate

Case 2 – Market interest rates drop to 4%

• New bonds only pay $40/year
• Our bond pays $50, which is better, so people are willing to pay more for it
• Price rises until our bond’s yield falls to 4%, aligning with the new market rate
• Price rises –> YTM falls to match market rate

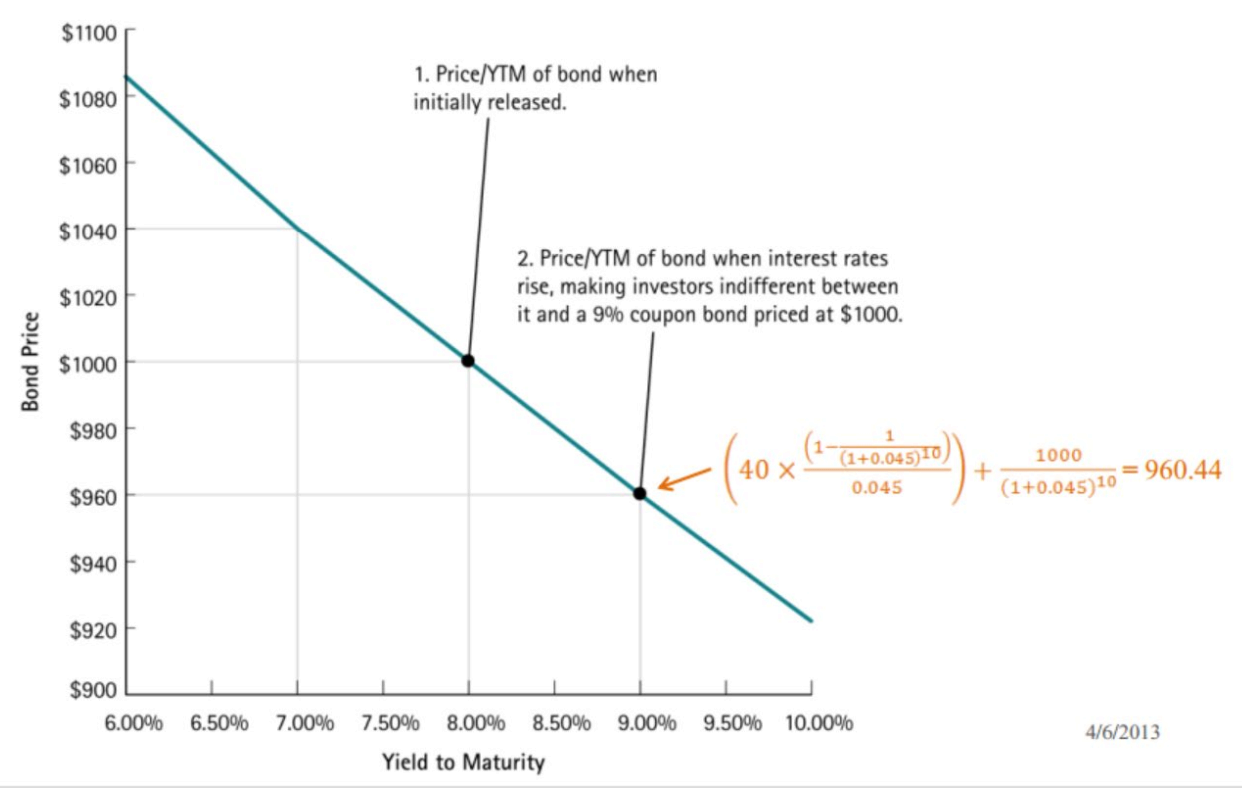
Example: Suppose an 8% semi-annual coupon US treasury bond was just sold at par at issuance. However, the Federal Reserve Bank’s fed fund rate suddenly rises to 9%.

1. What will be the rate of return on the bond now? The current YTM of the bond must be the same as the current interest rate in the market, i.e. 9%.
2. What will be the current price of the bond? The current price will equal the present value of the future cash flows discounted at the going market rate.

Bond Pricing Principle

Bond pricing is based on the basic principle on valuing the PV of known cash flows.

• A change in market interest rate causes a change in the opposite direction in the market values of fixed income securities.
  • Inverse relationship between $P and r%

Implications:

• Because interest rates are unpredictable, prices of fixed income securities are uncertain up to the time they mature.
• Bonds do not “guarantee” a fixed return
• Fixed income does not mean fixed return!

Why do bond prices change? The level of market interest has changed, but the promised future cash flows from the bond do not. A higher YTM implies a higher discount rate for a bond’s remaining cash flows, reducing their PV and hence the bond’s price. Thus, the price will fall to the point where it equals the PV of future values discounted at the prevailing interest rate.

• Bond prices subject to the effects of both the passage of time and changes in interest rate.
• Capital gain/loss yield = $\Delta \text{Price}/\text{Original Price}$.

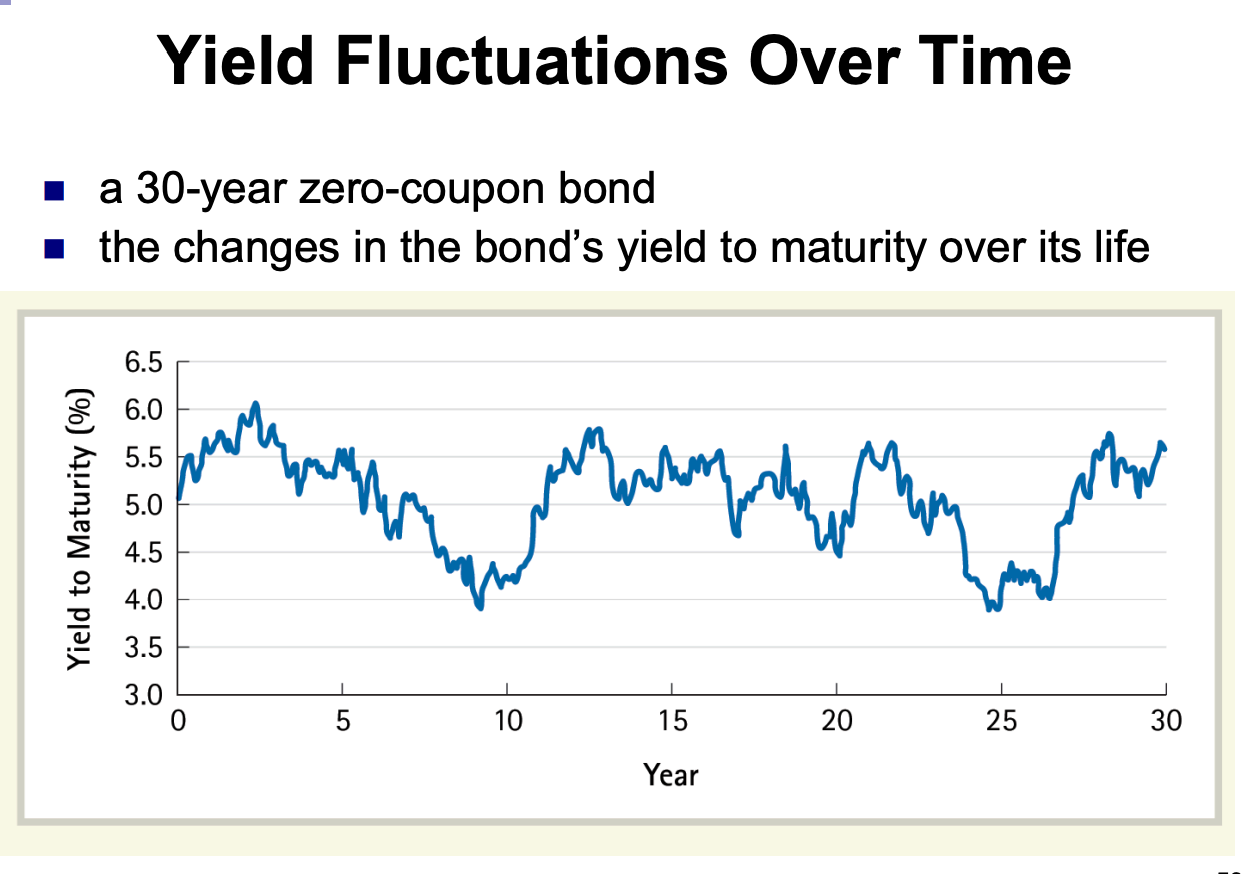
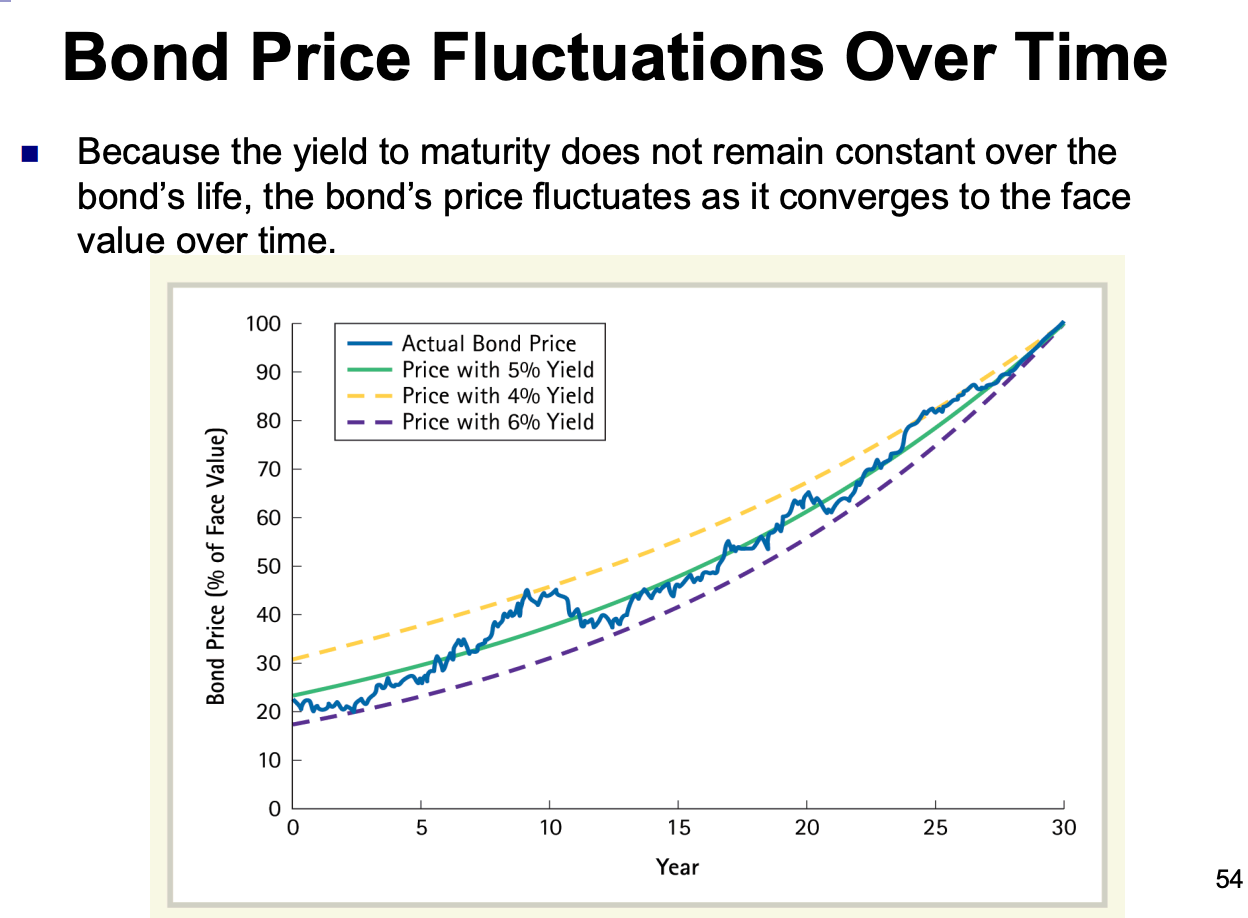
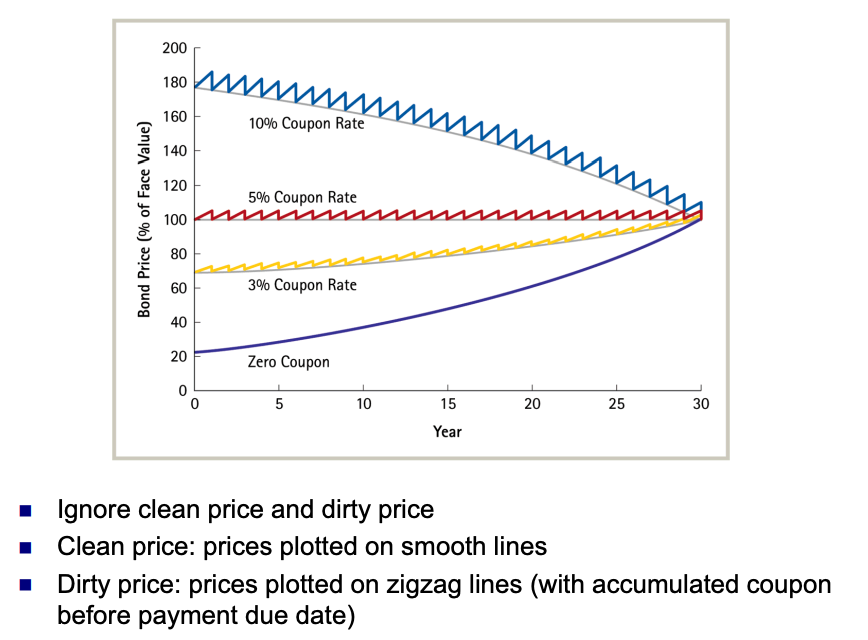
Time and Bond Prices

Suppose you purchase a 30-year, zero-coupon bond with a YTM of 5%. For a face value of $100, the bond will initially trade for

$$P(\text{30 years to maturity})=\frac{100}{1.05^{30}}=\$23.14$$

If the bond’s yield to maturity remains at 5%, what will its price be five years later? If you purchased the bond at $23.14 and sold it five years later, what would be the rate of return for your investment?

First, we can find:

$$P(\text{25 year to maturity})=\frac{100}{1.05^{25}}=\$29.53$$

and then:

$$\text{IRR}={\left(\frac{29.53}{23.14}\right)}^{\frac{1}{5}}-1=5.0\%$$

• Our return is the same as the YTM of the bond.
• Note that when there is less time to maturity, bond price goes up.
• The discount from its face value shrinks because there is less time until the face value will be received, but the yield has not changed.
• A bond’s yield to maturity is the rate of return of the bond. If the yield stays the same, your return also stays the same as the original yield when you first purchased the bond, even if you sell the bond before its maturity.
• If the yield stays the same, the price of discount or premium bond will move towards par value over time.

Example: A currently 20-year bond with a coupon rate of 12% paid semi-annually was sold at a premium 2 years ago at a price of $\mathrm{1171.59.}Itsparvalueis$1,000. Assume the YTM has been the same and remains unchanged.

• What is its YTM? Less than 12%, more than 12%, or exactly equal? Since the bond was sold at a premium, the YTM has to be less than 12%. If coupon > YTM, investors are receiving more interest than the prevailing market requires.
• What would the current market price be compared to the price 2 years ago? No change, decrease, or increase? The bond keeps paying the same high coupon, but there’s less time to collect the above-market coupons, so it’s worth less now than 2 years ago.

Interest Rate Sensitivity

The price of a bond is determined by three factors: time to maturity, coupon payment, and interest rate.

Interest rate sensitivity refers to the changes in the bond’s price due to changes in interest rate. This is affected by the timing and amount of the bond’s cash flows.

In general:

• Shorter maturity bonds have lower interest rate risk compared to longer maturity bonds.
• Bonds of higher coupon rates have lower interest rate risk compared to bonds of lower coupon.

Maturity Term and Interest Rate Risk

Thus, bonds with high duration are highly sensitive to interest rate changes, and vice versa. Essentially, longer period just means more compounding which results in larger change.

Example: Consider a 10-year coupon bond and a 30-year coupon bond, both with 10% annual coupons. By what percentage will the price of each bond change if their yield to maturity increases from 5% to 6%?

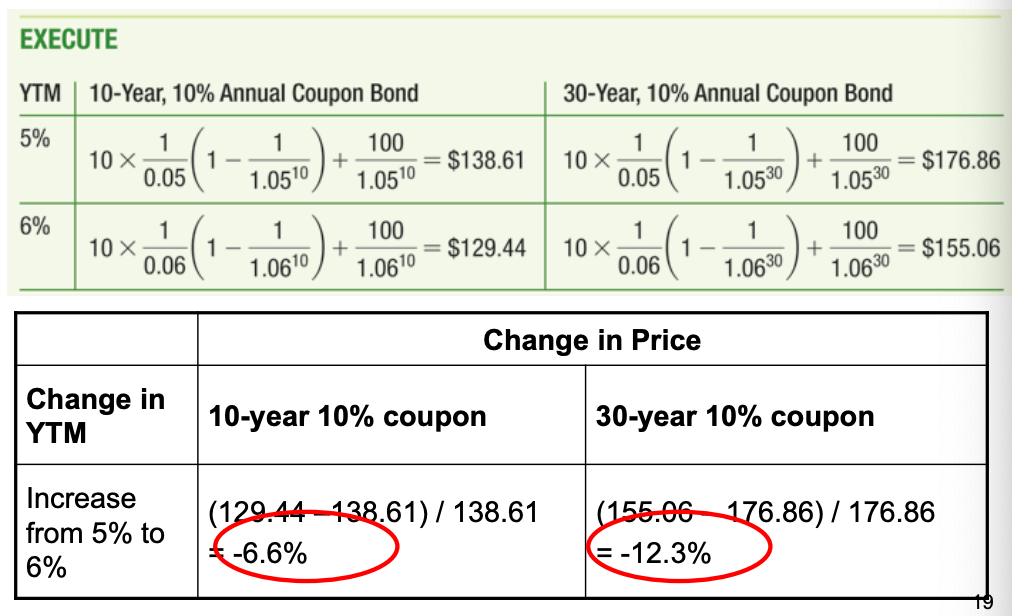
The 30-year coupon bond has a larger price drop. It is twice as sensitive as the 10-year bond to a change in the yield.

Coupons and Interest Rate Risk

A larger portion of the cash flows to be received in the future will result in larger changes in the PV when interest rate changes.

Example: Consider two bonds, each pays semi-annual coupons and 5 years left until maturity. One has a coupon rate of 5% and the other has a coupon rate of 10%, but both currently have a yield to maturity of 8%. How much will the price of each bond change if its yield to maturity decreases from 8% to 7%?

The 5% coupon bond’s price increased 4.4% and the 10% coupon bond increased 4.0%. Thus, the bond with smaller coupon payments is more sensitive to changes in interest rates.

• For low coupon bonds, coupons are smaller relative to its par value. So a larger fraction of its cash flows are received from its par value payment at maturity.
• PV of later cash flows are affected more greatly by changes in interest rates